Interpolation

Given a set of values for x in [x₁, x₂] and F(x), interpolation can be used to estimate a value of F(x) for any value of x in [x₁, x₂]. The figure below shows how to interpolate using Lagrange formula.

Dato un conjunto de valores para x en [x₁, x₂] y F(x), la interpolación se puede usar para estimar un valor de F(x) para cualquier valor de x en [x₁, x₂]. La figura de abajo muestra como interpolar usando la fórmula de Lagrange.

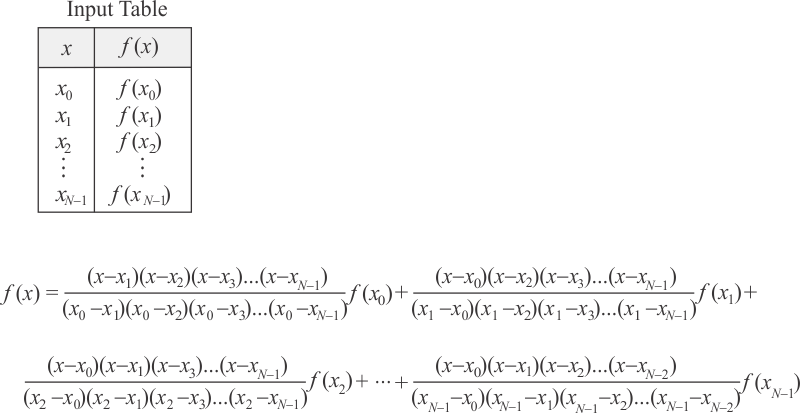
Problem 1

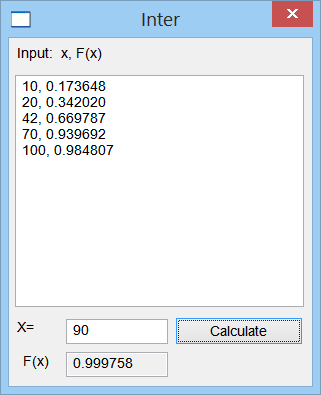
Cree a program called Inter using Wintempla to test Lagrange Interpolation.

Cree un programa llamado Inter usando Wintempla para probar la interpolación de Lagrange.

Inter.cpp

...
void Inter::Window_Open(Win::Event& e)
{

}

void Inter::btCalculate_Click(Win::Event& e)
{
     const double x = tbxX.DoubleValue;
     MATRIX table;
     Sys::Convert::ToMatrix(tbxInput.Text, table);
     tbxFx.DoubleValue = Math::Interpolation::Lagrange(table, x);
}

Neville's Algorithm

It is a recursive algorithm used for polynomial interpolation as shown in the figure below.

Es un algoritmo recursivo usado para interpolación polinomial como se muestra en la figura de abajo.

Problem 2

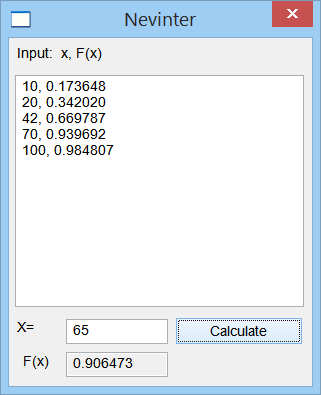
Cree a program called Nevinter using Wintempla to test Neville's algorithm.

Cree un programa llamado Nevinter usando Wintempla para probar el algoritmo de Neville.

Nevinter.cpp

...
void Nevinter::Window_Open(Win::Event& e)
{
}

void Nevinter::btCalculate_Click(Win::Event& e)
{
     const double x = tbxX.DoubleValue;
     MATRIX table;
     Sys::Convert::ToMatrix(tbxInput.Text, table);
     tbxFx.DoubleValue = Math::Interpolation::Neville(table, x);
}

Problem 3

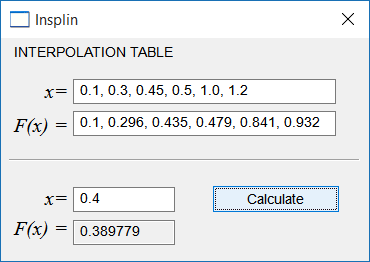
Cree a program called Insplin using Wintempla to interpolate using Splines.

Cree un programa llamado Insplin usando Wintempla para interpolar usando Splines.

Insplin.cpp

...
void Insplin::Window_Open(Win::Event& e)
{
}

void Insplin::btCalculate_Click(Win::Event& e)
{
     valarray<double> tableX, tableFx;
     Sys::Convert::ToVector(tbxTableX.Text, tableX);
     Sys::Convert::ToVector(tbxTableFx.Text, tableFx);
     Math::SplineInterpolation si;
     if (si.Create(tableX, tableFx) == false)
     {
          this->MessageBox(L"Unable to create Spline Interpolation", L"Insplin", MB_OK | MB_ICONERROR);
          return;
     }
     tbxFx.DoubleValue = si.Interpolate(tbxX.DoubleValue);
}

Interpolation in two dimensions

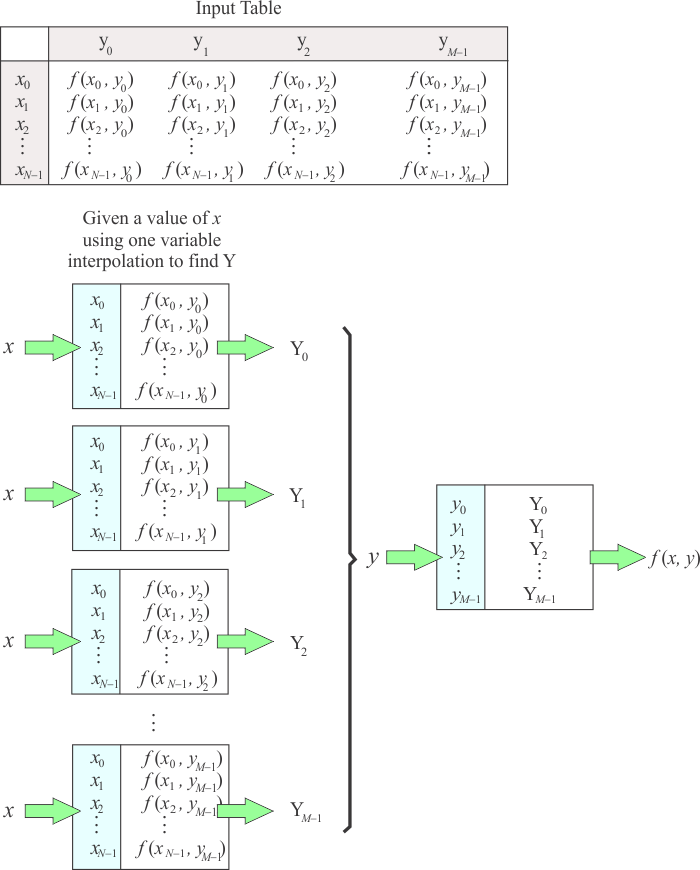
It is possible to extend Lagrange (or Neville) interpolation to two, three or more dimensions. The figure below illustrates how to interpolate in two dimensions.

Es posible extender la interpolación de Lagrange (o de Neville)a dos, tres o más dimensiones. La figura de abajo ilustra como interpolar en dos dimensiones.

Problem 4

Create an application called Surfen using Wintempla to interpolate in two dimensions the function f(x, y) = sin(x) + cos(y) +xy. The interpolation should be valid from -1 to 1 for both x and y. Use Neville's algorithm.

Cree una aplicación llamada Surfen usando Wintempla para interpolar en dos dimensiones la función f(x, y) = sin(x) + cos(y) +xy. La interpolación debe ser válida desde -1 a 1 para ambos x y y. Use el algoritmo de Neville.

Surfen.h

#pragma once //______________________________________ Surfen.h
#include "Resource.h"
class Surfen: public Win::Dialog
{
public:
     Surfen()
     {
     }
     ~Surfen()
     {
     }
     valarray<double> x;
     valarray<double> y;
     MATRIX f;
     ...
};

Surfen.cpp

...
void Surfen::Window_Open(Win::Event& e)
{
     const int N = 20;
     const double delta = 2.0/(N-1);
     //___________________________________________ Memory allocation
     x.resize(N);
     y.resize(N);
     Math::Oper::CreateMatrix(f, N, N);
     //________________________________________ Compute x, y and f(x, y) = sin(x) + cos(y) + x*y
     int i, j;
     for (i = 0; i < N; i++)
     {
          x[i] = -1.0 + delta*i;
          for (j = 0; j < N; j++)
          {
               y[j] = -1.0 + delta*j;
               f[i][j] = sin(x[i]) + cos(y[j]) +x[i]*y[j];
          }
     }
}

void Surfen::btInterpolate_Click(Win::Event& e)
{
     Win::HourGlassCursor hgc(true);
     const double input_x = tbxX.DoubleValue;
     const double input_y = tbxY.DoubleValue;
     tbxFxy.DoubleValue = Math::Interpolation::Neville2D(x, y, f, input_x, input_y);
}

Problem 5

Repeat the previous problem using Splines in 2D; called your program Spline2D.

Repita el problema anterior usando Splines en 2D; llame a su programa Spline2D.

Spline2D.h

#pragma once //______________________________________ Spline2D.h
#include "Resource.h"
class Spline2D: public Win::Dialog
{
public:
     Spline2D()
     {
     }
     ~Spline2D()
     {
     }
     Math::SplineInterpolation2D si;
protected:
     ...
};

Spline2D.cpp

...
void Spline2D::Window_Open(Win::Event& e)
{
     valarray<double> x;
     valarray<double> y;
     MATRIX f;

     const int N = 20;
     const double delta = 2.0/(N-1);
     //___________________________________________ Memory allocation
     x.resize(N);
     y.resize(N);
     Math::Oper::CreateMatrix(f, N, N);
     //________________________________________ Compute x, y and f(x, y) = sin(x) + cos(y) + x*y
     int i, j;
     for (i = 0; i < N; i++)
     {
          x[i] = -1.0 + delta*i;
          for (j = 0; j < N; j++)
          {
               y[j] = -1.0 + delta*j;
               f[i][j] = sin(x[i]) + cos(y[j]) +x[i]*y[j];
          }
     }
     if (si.Create(x, y, f) == false)
     {
          this->MessageBox(L"Unable to create Math::SplineInterpolation2D", L"Spline2D", MB_OK | MB_ICONERROR);
     }
}

void Spline2D::btInterpolate_Click(Win::Event& e)
{
     Win::HourGlassCursor hgc(true);
     const double input_x = tbxX.DoubleValue;
     const double input_y = tbxY.DoubleValue;
     tbxFxy.DoubleValue = si.Interpolate(input_x, input_y);
}

Interpolation

Interpolation

Neville's Algorithm

Interpolation in two dimensions

© Copyright 2000-2021 Wintempla selo. All Rights Reserved. Jul 22 2021. Home