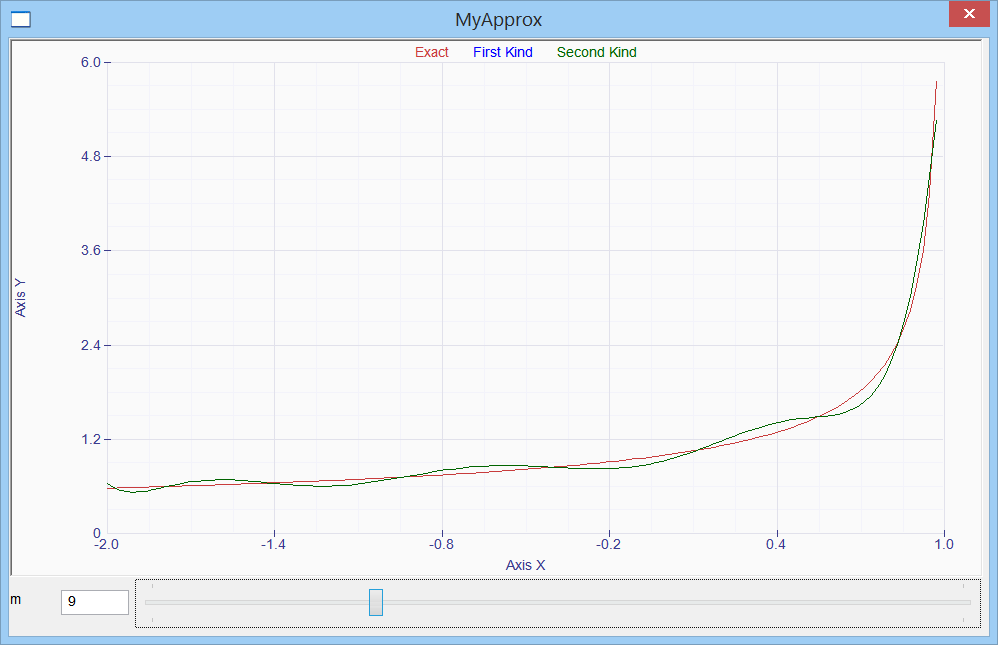
Chebyshev approximation |
| It can be used to approximate a function using Chebyshev polynomials of the first kind, Tn. The figure below shows how to evaluate these polynomials. You may inspect the Math::Chebyshev class to know more about Chebyshev polynomials. Thus, it is possible to approximate a continuous and bounded function f(x) in a given interval [a, b] as shown below where cn are called Chebyshev coefficients. (See: A method for numerical integration on an automatic computer. C.W. Clenshaw and A. R. Curtis, Numerische Mathematik 1960.) Esta puede ser usada para aproximar una función usando los polinomios de Chebyshev de la primera clase, Tn. La figura de abajo muestra como evaluar estos polinomios. Usted puede inspeccionar la clase Math::Chevyshev para conocer más acerca de los polinomios de Chebyshev. Así, es posible aproximar una función continua y acotada f(x) en un intervalo dado [a, b] como se muestra debajo donde cn son llamados los coeficientes de Chebyshev. (Ver: A method for numerical integration on an automatic computer. C.W. Clenshaw and A. R. Curtis, Numerische Mathematik 1960.) |



| Problem 1 |
| Create a Wintempla dialog application called MyApprox to approximate the function shown. Cree una aplicación de diálogo de Wintempla llamada MyApprox para aproximar la función mostrada. |
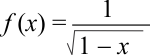
| MyApprox.h |
| #pragma once //______________________________________ MyApprox.h #include "Resource.h" #define POINT_COUNT 128 class MyApprox: public Win::Dialog, public Math::IFunction { public: MyApprox() { a = -2.0; b = 0.97; } ~MyApprox() { } double a; double b; valarray<double> c1, c2; double EvaluateFunc(const double x); void Refresh(); protected: ... }; |
| MyApprox.cpp |
| ... void MyApprox::Window_Open(Win::Event& e) { const int N = 30; Math::Chebyshev::ComputeCoefficients_FirstKind(*this, a, b, N, c1); Math::Chebyshev::ComputeCoefficients_SecondKind(*this, a, b, N, c2); //________________________________________________________ sldM sldM.SetRange(1, N); sldM.Position = N/2; tbxM.IntValue = N/2; //________________________________________________________ xyMain xyMain.CaptionX = L"Axis X"; xyMain.CaptionY = L"Axis Y"; xyMain.MinX=-2.0; xyMain.MaxX= 1.0; xyMain.MinY= 0.0; xyMain.MaxY= 6.0; xyMain.Graphs.Add(POINT_COUNT); xyMain.Graphs.Add(POINT_COUNT); xyMain.Graphs.Add(POINT_COUNT); const double deltaX = (b - a) / (POINT_COUNT -1.0); double x; for(int i=0; i<POINT_COUNT; i++) { x = a + i*deltaX; xyMain.Graphs[0][i].x = x; xyMain.Graphs[1][i].x = x; xyMain.Graphs[2][i].x = x; // xyMain.Graphs[0][i].y = EvaluateFunc(x); } xyMain.Graphs[1].Color = RGB(0, 0, 255); xyMain.Graphs[2].Color = RGB(0, 100, 0); xyMain.Graphs[0].Caption = L"Exact"; xyMain.Graphs[1].Caption = L"First Kind"; xyMain.Graphs[2].Caption = L"Second Kind"; Refresh(); } void MyApprox::sldM_Hscroll(Win::Event& e) { const int position = sldM.HasPositionChanged(); if (position < 0) return; tbxM.IntValue = position; Refresh(); } void MyApprox::Refresh() { const int m = tbxM.IntValue; double x; for(int i=0; i<POINT_COUNT; i++) { x = xyMain.Graphs[0][i].x; // xyMain.Graphs[1][i].y = Math::Chebyshev::ComputeApproximation_FirstKind(a, b, c1, m, x); xyMain.Graphs[2][i].y = Math::Chebyshev::ComputeApproximation_SecondKind(a, b, c2, m, x); } xyMain.RefreshAll(); } double MyApprox::EvaluateFunc(const double x) { return 1.0/sqrt(1.0 - x); } |