Genetic Algorithm |
| A Genetic Algorithm (GA) is optimization method inspired in the process of evolution. The process of evolution is based on the genetic structure of the individuals; this structure affects how well an individual can adapt to their environment. Una Algoritmo Genético (AG) es un método de optimización inspirado en el proceso de la evolución. El proceso de la evolución está basado en la estructura genética de los individuos; esta estructura afecta como los individuos se adaptan a su ambiente. |
| Problem 1 |
| Find the values of x and y in the following system of equations. |
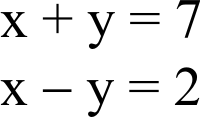
Coding |
| In order to use GA to solve an optimization problem, the solution of the problem must be code using zeros and ones to represent the genes of the individual. In the previous problem, this implies that we must represent the values x and y as as sequence of ones and zeros. First, we need to determine how many bits must be used for each variable; in this case (for clarity purposes) we will restrict the optimization to integer values from 0 to 15. Thus, 4 bits (24 = 16) are required to represent the 16 integer values. Second, we need to compute the total number of bits to store a solution, in this case a solution will require a total of 8 bits: 4 bits for x and 4 bits for y. The figure below shows the coding for several random values of x and y. A fin de usar un AG para resolver un problema de optimización, la solución del problema debe ser codificada usando ceros y unos para representar los genes de los individuos. En el problema previo, esto implica que nosotros debemos representar los valores de x y y como una secuencia de unos y ceros. Primero, necesitamos determinar cuántos bits deben ser usados para cada variable; en este caso (para propósitos de claridad) nosotros restringiremos la optimización a valores enteros desde 0 a 15. Así, 4 bits (24 = 16) son requeridos para representar los 16 valores enteros. Segundo, necesitamos calcular el número total de bits para almacenar la solución, en este caso una solución requerida un total de 8 bits: 4 bits para x y 4 bits para y. La figura de abajo muestra la codificación para varios valores aleatorios de x y y. |

Fitness |
| Each individual has fitness or a value that indicates how close to a desired value an individual is. Usually, some sort of error such as mean squared error can be used to compute the fitness. However, it is very important to notice that an individual with small mse will have a high value of fitness. The figure below shows the mse and fitness for each individual. In this specific example, the fitness is computed as the inverse of the mse, but other more complex algorithms are recommended. Observe that a value of 0.001 was added to the mse to avoid division by zero. Cada individuo tiene un grado de adaptabilidad o valor que indica que tan cerca de un valor deseado un individuo está. Usualmente, algún tipo de error tal como error medio cuadrático puede ser usado para calcular el grado de adaptabilidad. Sin embargo, es muy importante observar que un individuo con un mse pequeño tendrá un alto valor en su grado de adaptabilidad. En este ejemplo específico, el grado de adaptabilidad se calculó como el inverso del mse, pero otros algoritmos más complejos son recomendados. Observe que un valor de 0.001 fue sumado al mse para evitar la división entre cero. |
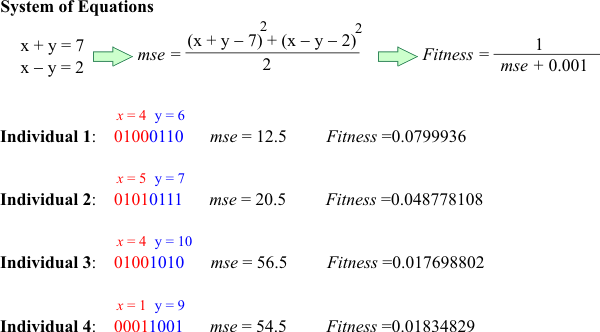
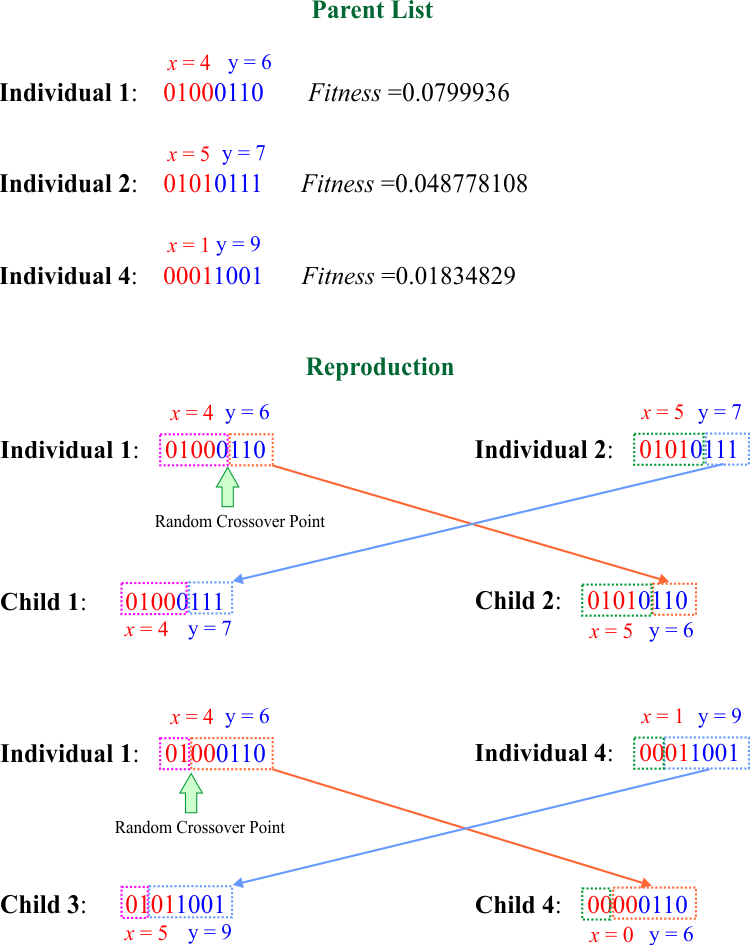
Parent Selection |
| Once the fitness value for each individual has been computed, the next step is to choose the parents to create the individuals of the next generation. There are several methods to choose the parents; however, all of these methods try to choose the individuals with the highest fitness. Additionally, the number of parents must guarantee that the number of individuals in the next generation is equal to the number of individuals in the current generation. The figure below shows the four individuals of the current generation. First, we find the fitness for each individual. Second, we discard the individual 3 because its fitness is low. The rest of the individuals will be the parents; in this case the individual 1 (with the highest fitness) will be used twice. Una vez que el grado de adaptabilidad se ha calculado para cada individuo, el próximo paso es escoger a los padres para crear los individuos de la próxima generación. Hay varios métodos para escoger a los padres; sin embargo, todos estos métodos tratan de escoger a los individuos con los mayores grados de adaptabilidad. Adicionalmente, el número de padres debe garantizar que el número de individuos en la próxima generación sea igual al número de individuos en la generación actual. La figura de bajo muestra los cuatro individuos de la generación actual. Primero, encontramos el grado de adaptabilidad para cada individuo. Segundo, nosotros descartamos el individuo 3 porque tiene un grado de adaptabilidad bajo. El resto de los individuos serán los padres; en este caso el individuo 1 (con el grado de adaptabilidad más alto) se usará dos veces. |

Reproduction |
| The figure below shows how reproduction works. From two parents, two children are created. First, a random point called crossover point is generated. Second, the crossover point creates two sequences of bits in each parent. Finally, the first child is produced by combining the first sequence from the one the parents and the second sequence form the other parent. The second child is produced using the other sequences from the parents that were not used in the first child. In the example below, the children 1 and 2 are created from the individuals 1 and 2; the children 3 and 4 are created from the individual 1 and 4. The probability of crossover is used to determine how many children will be created from the parents. Usually the probability of crossover takes values around 0.8. La figura de abajo muestra cómo trabaja la reproducción. Desde los dos padres, se crean dos niños. Primero un punto aleatorio llamado punto de crossover es generado. Segundo, el punto de crossover crea dos secuencias de bits en cada padre. Finalmente, el primer niño es producido combinando la primera secuencia de uno de los padres y la segunda secuencia del otro padre. El segundo niño se produce usando las otras secuenciad de los padres que no fueron usados en el primer niño. En el ejemplo de abajo, los niños 1 y 2 fueron creados usando los individuos 1 y 2; los niños 3 y 4 fueron creados usando los individuos 1 y 4. La probabilidad de crossover es usada para determinar cuántos niños se crearán desde los padres. Usualmente la probabilidad de crossover toma valores alrededor de 0.8 |
Mutation |
| From generation to generation, it is very possible that the individual are very similar. To solve this problem, GA introduces mutation which is the flipping of one random bit (gene). The probability of mutation is used to know how many bits should be flipped. Usually the probability of mutation takes values around 0.01. This means that mutation is very rare event. The figure below shows how mutation works. Desde una generación a otra, es muy posible que los individuos sean muy similares. Para resolver este problema, AG introduce la mutación la cual consiste en invertir un bit aleatorio (gene). La probabilidad de mutación es usada para saber cuántos bits deben ser invertidos. Usualmente la probabilidad de mutación toma valores alrededor de 0.01. Esto significa que la mutación es un evento muy raro. La figura de abajo muestra cómo funciona la mutación. |

Generation |
| The method of GA begins by creating a pool (set) of random individuals. The individuals with the highest fitness are chosen as parents. Children are created to replace the previous generation. If one (or more) parent has a higher fitness than the children, he (or they) can become individuals in the next generation. The method stops when one of the individuals has a desired fitness. El método de AG comienza creando un conjunto de individuos aleatorios. Los individuos con los grados más altos de adaptabilidad se escoben para ser padres. Los niños se crean para reemplazar a la generación previa. Si un (o más) padre tiene un grado de adaptabilidad más alto que los niños, el (o ellos) pueden ser individuos en la próxima generación. El método se detiene cuando uno de los individuos tiene un grado de adaptabilidad deseado. |
Genetic Algorithm Requirements |
In order to use GA to solve a problem, there are three requirements that the problem must meet:
A fin de usar AG para resolver un problema, hay tres requisitos que el problema debe cumplir:
|
| Problem 2 |
| Find the minimum of equation shown below using Genetic Algorithm, Microsoft Visual Studio and Wintempla. Create a Window Application called MiniGA using Wintempla as shown use the Genetic Algorithm Application option. |
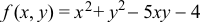
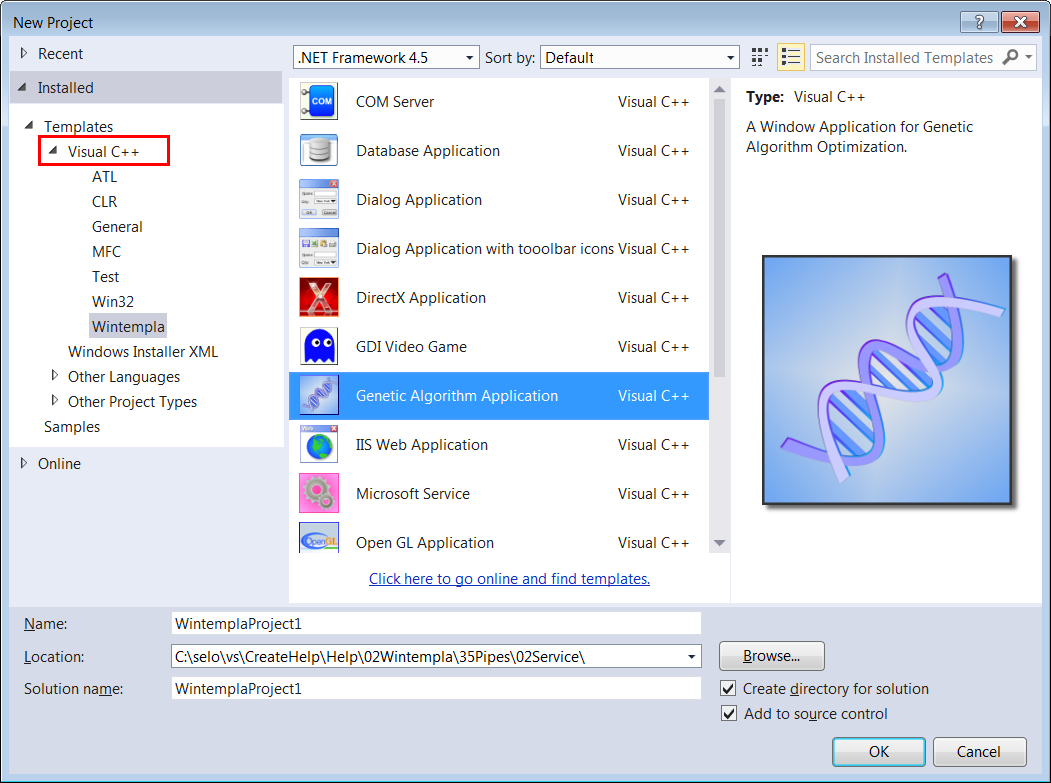
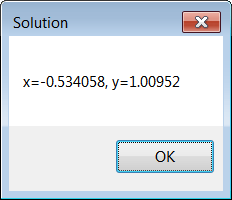
| Solution 1 |
Wintempla will generate a multi-thread program with a basic configuration to perform the optimization. You may edit the Solution.h and Solution.cpp files to customize the optimization. The wizard provides some sample code to minimize the equation of the problem; so you not need to edit any code for this example. You must, however, edit these files for other optimization problems. As a matter of fact, you must provide code to perform the following four steps:
Wintempla generará un programa multi-tarea con una configuración básica para realizar la optimización. Usted puede editar los archivos Solution.h y Solution.cpp para personalizar la optimización. El asistente proporciona algunos códigos muestra para minimizar la ecuación del problema, así que usted no tiene que editar nada de código para este ejemplo. Usted debe, sin embargo, editar estos archivos para otros problemas de optimización. De hecho, usted debe proporcionar el código para realizar los cuatro pasos siguientes:
|
| Tip |
Observe the following key points in the program:
Observe los siguientes puntos claves en el programa:
|
| Tip |
| The GeneticGetError must return a value from 0 to 1. The function must be as smooth as possible (avoid discontinuities). La función GeneticGetError debe regresar un valor desde 0 a 1. La función debe ser tan suave como sea posible (evite las discontinuidades.) |