2D Array |
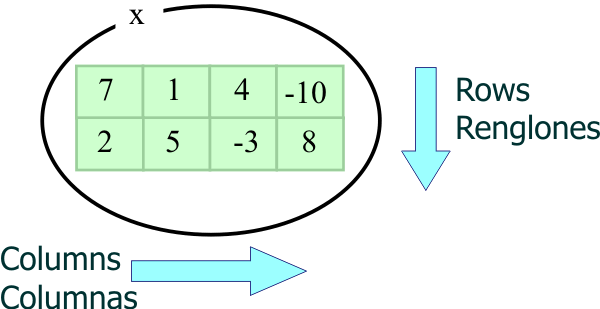
| A 2D array is an array of elements that is organized in a 2D space and requires two indexes to access the data or the objects in the array. The figure below shows a 2D array with two rows and four columns. A total of 8 integer values can be stored in the array. Un arreglo de dos dimensiones es un arreglo que está organizado en un espacio de dos dimensiones y requiere de dos índices para accesar los datos o los objetos en el arreglo. La figura de abajo muestra un arreglo de dos dimensiones con dos renglones y cuatro columnas. Un total de 8 valores enteros pueden ser almacenados en el arreglo. |
| Tip |
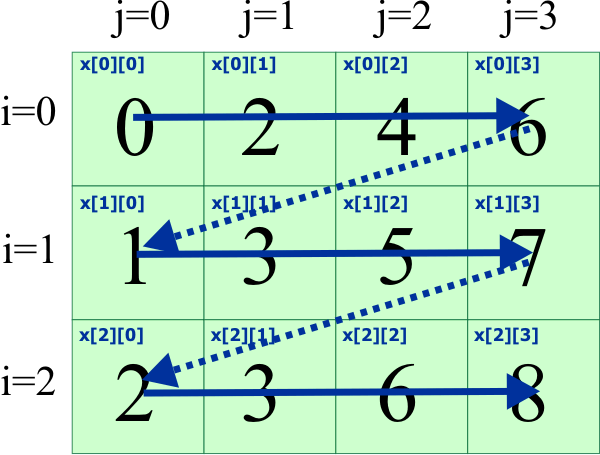
| An index (usually an integer value of name i) is used to navigate the rows using the instruction for. Another index (usually an integer value of name j) is used to navigate the columns using another instruction for. The example shown below illustrates how to declare a matrix (a 2D array) with three rows and four columns; the code sets the twelve integer values in the matrix in i+2*j. Un índice (usualmente un valor entero de nombre i) es usado para navegar los renglones usando la instrucción for. Otro índice (usualmente un valor entero de nombre j) es usado para navegar las columnas usando otra instrucción for. El ejemplo de abajo ilustra como declarar una matriz (un arreglo de 2 dimensiones) con tres renglones y cuatro columnas; el código fija el valor de los doce valores enteros en i+2*j. |
| Program.cpp |
| void Program::Window_Open(Win::Event& e) { int x[3][4]; int i, j; for(i = 0; i < 3; i++) //Rows - renglones { for(j = 0; j < 4; j++) //Columns - columnas { x[i][j] = i + 2*j; } } } |
| Tip |
| Arrays of more than 2 dimensions are not frequently used as they require a lot of memory. Los arreglos de más de dos dimensiones no son frecuentemente usados ya que requieren de grandes cantidades de memoria. |
| Problem 1 |
| Compute output of the code shown. Suppose there is a textbox called tbx1 with the property of multiline. Calcule la salida del código de abajo. Suponga que hay una caja de texto llamada tbx1 con la propiedad de multilínea. |
| Program.cpp |
| void Program::Window_Open(Win::Event& e) { wstring text; int i, j; int data[2][2]; for(i = 0; i<2; i++) // Rows - renglones { for(j = 0; j<2; j++) // Columns - columnas { if (i<=0) { data[i][j] = i+j; } else { data[i][j] = i-j; } Sys::Format(text, L"[%d][%d]=%d\t", i, j, data[i][j]); tbx1.Text += text; } tbx1.Text += L"\r\n"; } } |
| Problem 2 |
| Compute output of the code shown. Suppose there is a textbox called tbx1 with the property of multiline. Calcule la salida del código de abajo. Suponga que hay una caja de texto llamada tbx1 con la propiedad de multilínea. |
| Program.cpp |
| void Program::Window_Open(Win::Event& e) { wstring text; int i, j; int data[3][2]; for(i = 0; i<3; i++) // Rows - renglones { for(j = 0; j<2; j++) // Columns - columnas { if (i < j) { data[i][j] = 2*i; break; } data[i][j] = i - j; } } for(i = 0; i<3; i++) // Rows - renglones { for(j = 0; j<2; j++) // Columns - columnas { Sys::Format(text, L"[%d][%d]=%d\t", i, j, data[i][j]); tbx1.Text += text; } tbx1.Text += L"\r\n"; } } |
| Problem 3 |
| Compute output of the code shown. Suppose there is a textbox called tbx1 with the property of multiline. Calcule la salida del código de abajo. Suponga que hay una caja de texto llamada tbx1 con la propiedad de multilínea. |
| Program.cpp |
| void Program::Window_Open(Win::Event& e) { wstring text; int data[2][2]; int n = 0, i, j; for(i = 0; i<2; i++) { for(j = 0; j<2; j++) { data[i][j] = i + j; data[i][j] =2*i-j*3; } n = n + data[i][j-1]; } Sys::Format(text, L"[%d]", n); tbx1.Text = text; } |
A Matrix in STL |
| To create a matrix using the STL it is necessary to combine the vector and valarray templates. Wintempla defines MATRIX as vector of valarrays, that is #define MATRIX vector<valarray<double> >. The main advantage of using the STL to handle matrices is to be able to assign (or change) their size at run time without using pointes and dynamic memory. Para crear una matriz usando la STL es necesario combinar las plantillas de vector y valarray. Wintempla define MATRIX como un vector de valarrays, esto es #define MATRIX vector<valarray<double> >. La principal ventaja de usar la STL para manejar matrices es para poder asignar (o cambiar) el tamaño de la matriz en el momento de ejecución sin usar punteros y memoria dinámica. |
| Tip |
| The code shown below create a matrix with three rows and two columns using the STL. El código de abajo crea una matriz de tres renglones y dos columnas usando la STL. |
| Program.cpp |
| void Program::Window_Open(Win::Event& e) { //____________________________ Method 1 MATRIX y; y.resize(3); for(int i = 0; i<3; i++) y[i].resize(2); //____________________________ Method 2 MATRIX z; Math::Oper::CreateMatrix(z, 2, 3); //____________________________ Method 3 MATRIX z(3, valarray<double>(2)); //____________________________ Method 4 (It does not work any more) MATRIX x (3, 2); } |
| Tip |
| The code below illustrates how to create a matrix of integer values (using Java) with four rows and three columns, and a matrix of double values with three rows and two columns. El código de abajo muestra cómo crear una matriz de de enteros (usando Java) de cuatro renglones y tres columnas, y una matriz de valores punto flotante (double) de tres renglones y dos columnas. |
| Program.java |
| public class Program { public Program() { int [][] data = new int[4][3]; double matrix[][] = new double [3][2]; } }; |