Review

Tip

Always be careful when using array. The index of the array can go from zero to the number of element minus one. If you provide an invalid index, the program will produce an exception which will be displayed in a error message box. (Do not trespass your neighbor house)

Siempre tenga cuidado al usar los arreglos. El índice del arreglo puede ir desde cero hasta un menos el número de elementos del arreglo. Si usted proporciona un índice invalido, el programa originará una excepción la cual se mostrará en una caja de mensaje de error. (No te metas en la casa del vecino)

Problem 1

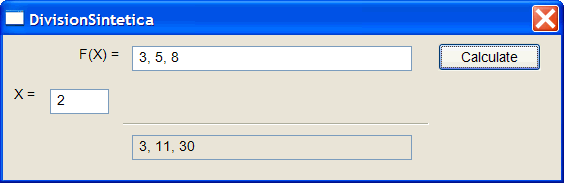
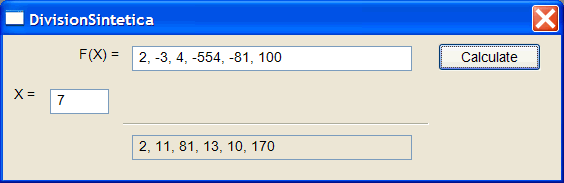
Write a program called DivisionSintetica to evaluate a polynomial.

Escriba un programa llamado DivisionSintetica para evaluar un polinomio.

DivisionSintetica.h

#pragma once //______________________________________ DivisionSintetica.h
#include "resource.h"
class DivisionSintetica: public Win::Dialog
{
public:
     DivisionSintetica()
     {
     }
     ~DivisionSintetica()
     {
     }
     void Division(double x, const valarray<double>& input, valarray<double>& output);
protected:
     ...
};

DivisionSintetica.cpp

void DivisionSintetica::Window_Open(Win::Event& e)
{
}

void DivisionSintetica::btCalculate_Click(Win::Event& e)
{
     valarray<double> input;
     valarray<double> output;

     Sys::Convert::ToVector(tbxInput.Text, input);
     Division(tbxX.DoubleValue, input, output);
     //______________________________________ Display the result
     wstring text;
     Sys::Convert::ToString(output, text);
     tbxOutput.Text = text;
}

void DivisionSintetica::Division(double x, const valarray<double>& input, valarray<double>& output)
{
}

Problem 2

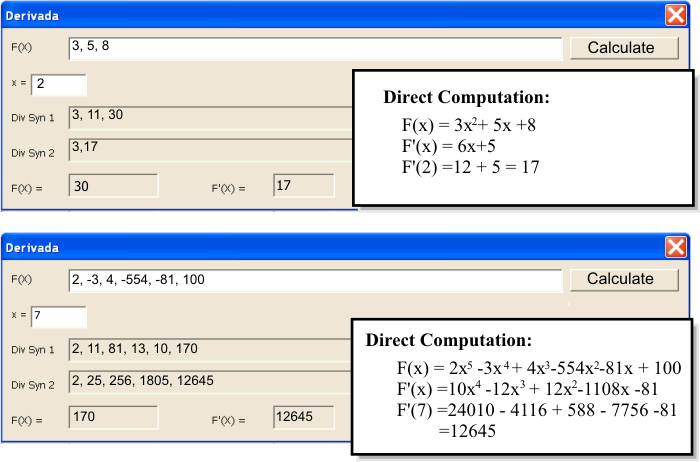
It is possible to evaluate the derivative of a polynomial by applying two synthetic divisions as shown. Create a program called Derivada to estimate the derivative of a polynomial for a value of x.

Es posible evaluar la derivada de un polinomio si se aplican dos divisiones sintéticas como se muestra. Cree un programa llamado Derivada para estimar la derivada de un polinomio para un valor de x.

Problem 3

Write a program called ProductoInterior to computer the inner product between two vectors.

Escriba un programa llamado ProductoInterior que calcula el producto interno entre dos vectores.

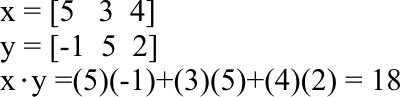
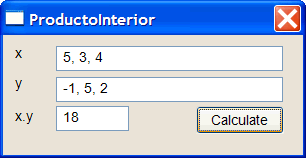
ProductoInterior.h

#pragma once //______________________________________ ProductoInterior.h
#include "resource.h"
class ProductoInterior: public Win::Dialog
{
public:
     ProductoInterior()
     {
     }
     ~ProductoInterior()
     {
     }
     double InnerProduct(const valarray<double>& x, const valarray<double>& y);
protected:
     ...
};

ProductoInterior.cpp

void ProductoInterior::Window_Open(Win::Event& e)
{
}

void ProductoInterior::btCalculate_Click(Win::Event& e)
{
     valarray<double> x, y;
     Sys::Convert::ToVector(tbxX.Text, x);
     Sys::Convert::ToVector(tbxY.Text, y);
     tbxResult.DoubleValue = InnerProduct(x, y);
}

double ProductoInterior::InnerProduct(const valarray<double>& x, const valarray<double>& y)
{
}

Problem 4

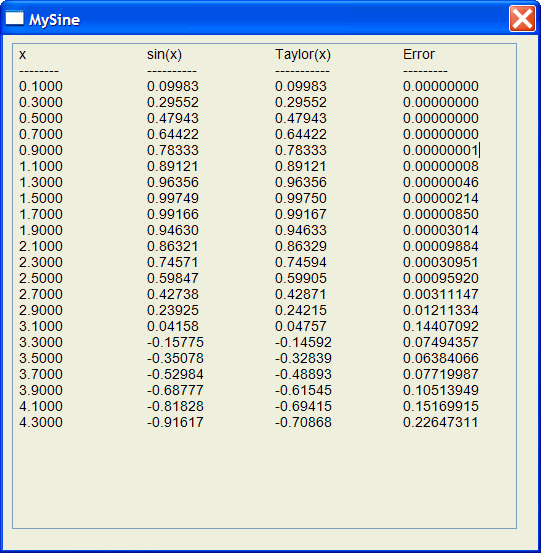
Write a program called MySine to estimate the value of sin(x) using Taylor's formula as shown in the example below for the sine of 0.5. Use only five terms in your program.

Escriba un programa llamado MySine para estimar el valor de sin(x) usando al fórmula de Taylor como se muestra en el ejemplo para el seno de 0.5. Use solamente cinco términos en su programa.

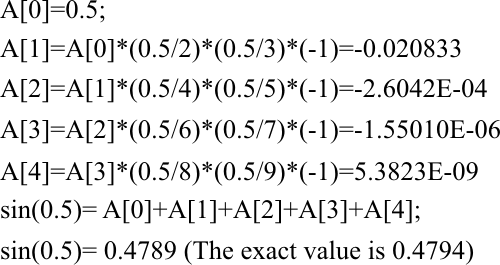
MySine.h

#pragma once //______________________________________ MySine.h
#include "resource.h"
class MySine: public Win::Dialog
{
public:
     MySine()
     {
     }
     ~MySine()
     {
     }
     double TaylorSine(double x);
protected:
     ...
};

MySine.cpp

void MySine::Window_Open(Win::Event& e)
{
     wstring text;
     double tsine = 0.0;
     double error = 0.0;
     ...
     for(double x = ...)
     {
          exact = sin(x);
          tsine = TaylorSine(x);
          error = fabs(exact - tsine) / fabs(exact );
          ...
     }
}

double MySine::TaylorSine(double x)
{
     ...
     return A.sum();
}

Problem 5

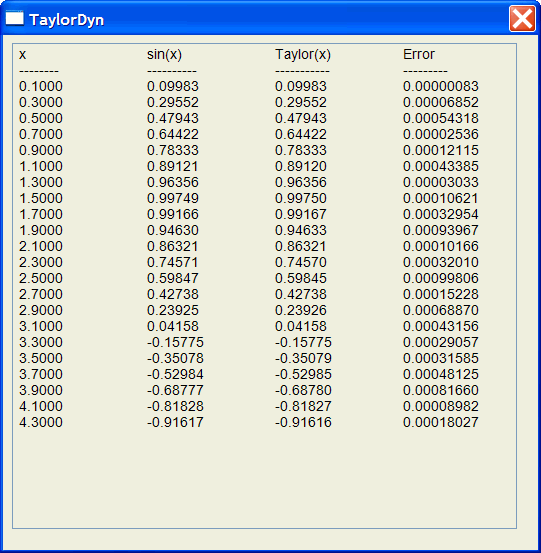
Write a program called TaylorDyn to estimate the value of sin(x) using Taylor's formula using a dynamic number of terms to have an error less than 0.001 as defined in the code shown below.

Escriba un programa llamado Taylor para estimar el valor del seno de x usando la fórmula de Taylor usando un número dinámico de términos para tener un error menor a 0.001 como se define en el código de abajo.

TaylorDyn.h

#pragma once //______________________________________ TaylorDyn.h
#include "resource.h"
class TaylorDyn: public Win::Dialog
{
public:
     TaylorDyn()
     {
     }
     ~TaylorDyn()
     {
     }
     double TaylorSine(double x, double& error);
protected:
     ...
};

TaylorDyn.cpp

void TaylorDyn::Window_Open(Win::Event& e)
{
     tbxOutput.Text = L"x\t\tsin(x)\t\tTaylor(x)\t\tError\r\n--------\t\t----------\t\t-----------\t\t---------\r\n";
     wstring text;
     double tsine = 0.0;
     double error = 0.0;
     for(double x = 0.1; x<= 4.5; x+= 0.2)
     {
          tsine = TaylorSine(x, error);
          Sys::Format(text, L"%.4f\t\t%.5f\t\t%.5f\t\t%.8f\r\n", x, sin(x), tsine, error);
          tbxOutput.Text += text;
     }
}

double TaylorDyn::TaylorSine(double x, double& error)
{
     double sum = x;
     double A = x;
     double nextA;
     error = 1.0e100;
     int i = 1;
     for(i = 1; i < 20; i++)
     {
          ...
          error = fabs(nextA/sum);
          if (error < 0.001) break;
     }
     return sum;
}

Problem 6

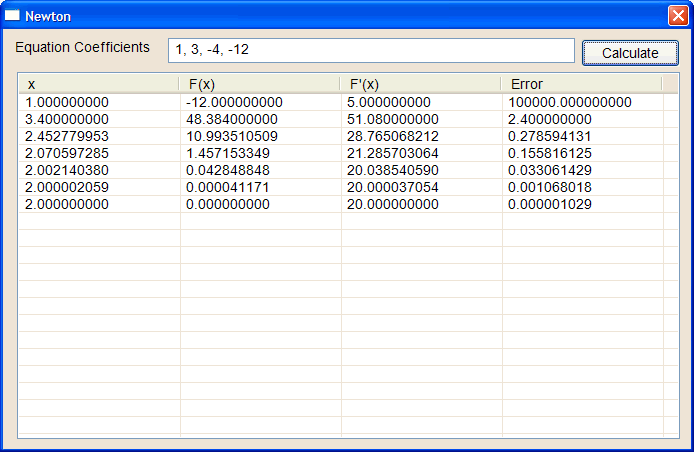
Write a program called Newton to find one solution of a polynomial using Newton formula and synthetic division. Use a value of one as the initial value of x. Note the problem uses a list view control, see the section Wintempla > GUI > List View to learn how to use the list view control.

Escriba un programa llamado Newton para encontrar una solución de una ecuación polinomial usando la fórmula de Newton y división sintética. Use un valor de uno como el valor inicial de x. Observe que el problema usa el control de list view, vea la sección Wintempla > GUI > List View para aprender a usar el control de list view.

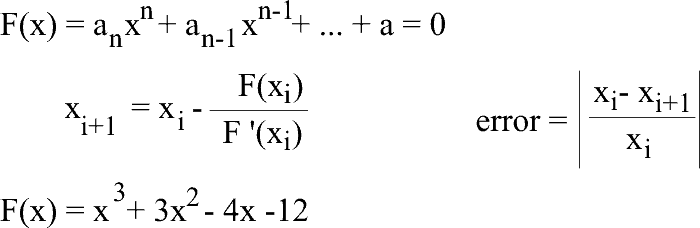
Newton.cpp

void Newton::Window_Open(Win::Event& e)
{
     //________________________________________________________ lvIteration
     const int columnWidth = (lvIteration.Width - 5 - Sys::Metrics::GetVScrollWidth())/4;
     ...
}

void Newton::btCalculate_Click(Win::Event& e)
{
     valarray<double> coeff;
     valarray<double> output;
     Sys::Convert::ToVector(tbxEquation.Text, coeff);
     double x = 1.0;
     double nextx = 1.0;
     wstring text;
     double fx = 1.0;
     double dx = 0.0;
     double error = 1.0e100;
     for(int i = 0; i <1000; i++)
     {
          fx = ...;
          dx = ...;
          ...
          error = fabs((x-nextx)/x);
          //
          if (error < 1.0e-7) break;
     }
}

Review

© Copyright 2000-2021 Wintempla selo. All Rights Reserved. Jul 22 2021. Home