| Tip |
| This section will solve the same problem using a regular ANN and a complex domain ANN. A training set and a validation set are built to use for both ANNs. For the first case, the training set is transform using the FFT, however, as the regular ANN cannot accept complex domain inputs, one neuron will accept the real part of one complex number, and another neuron will accept the imaginary part of the same complex number. On the other hand, the complex domain ANN can accept directly a complex domain number. Generally speaking, the complex domain ANN requires half the number of neurons than a regular ANN. Note however, that even though the complex domain ANN requires also half the number of weights than a regular ANN, each weight has a real part and an imaginary part. |
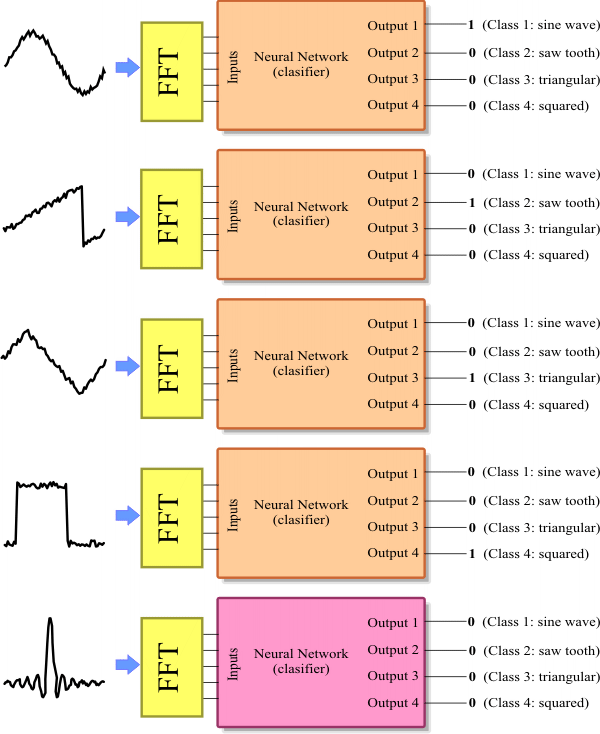
| Problem 1 |
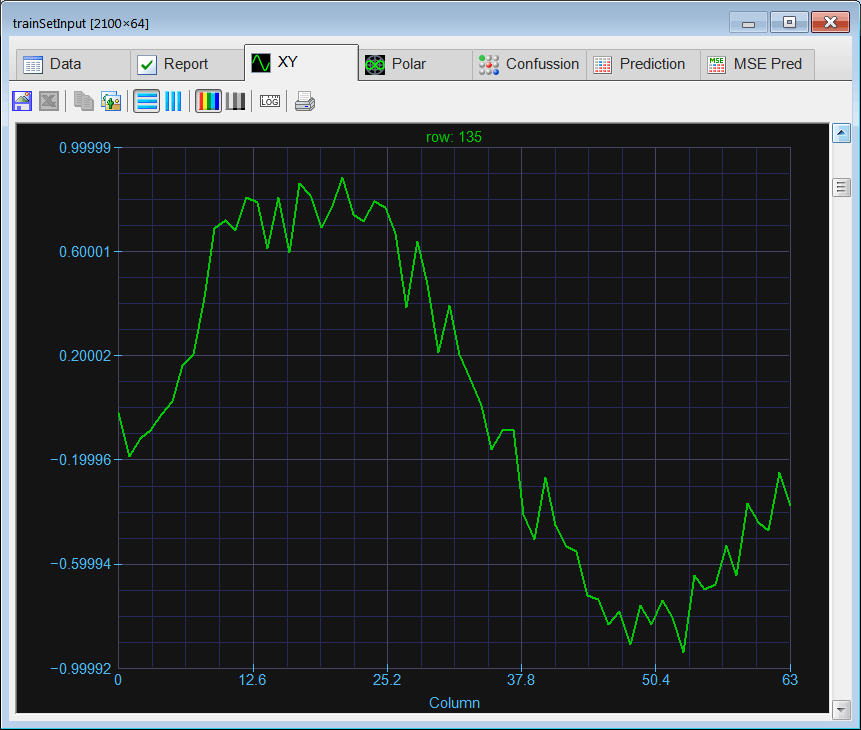
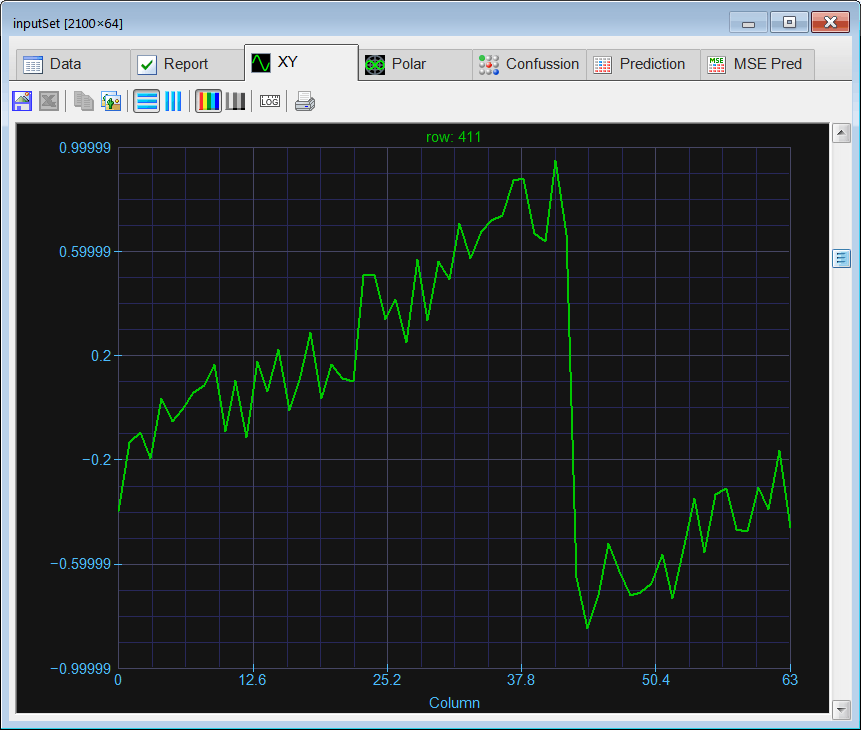
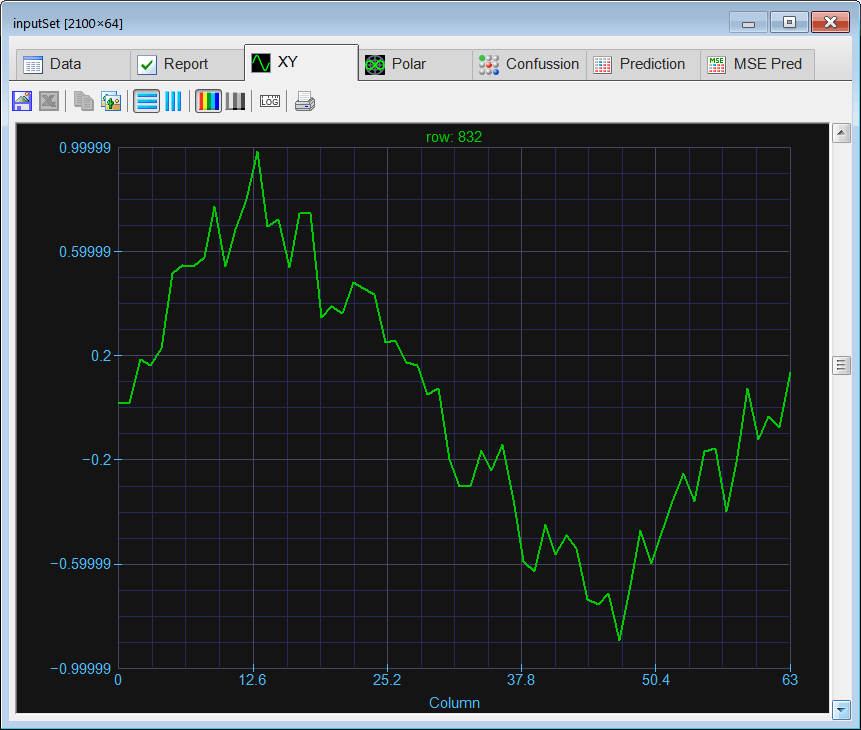
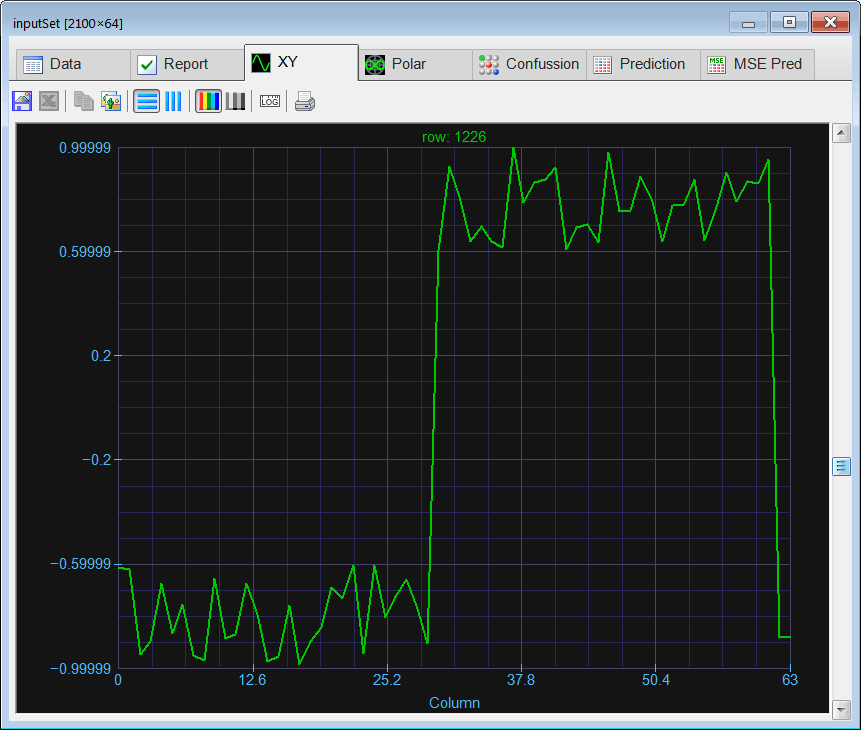
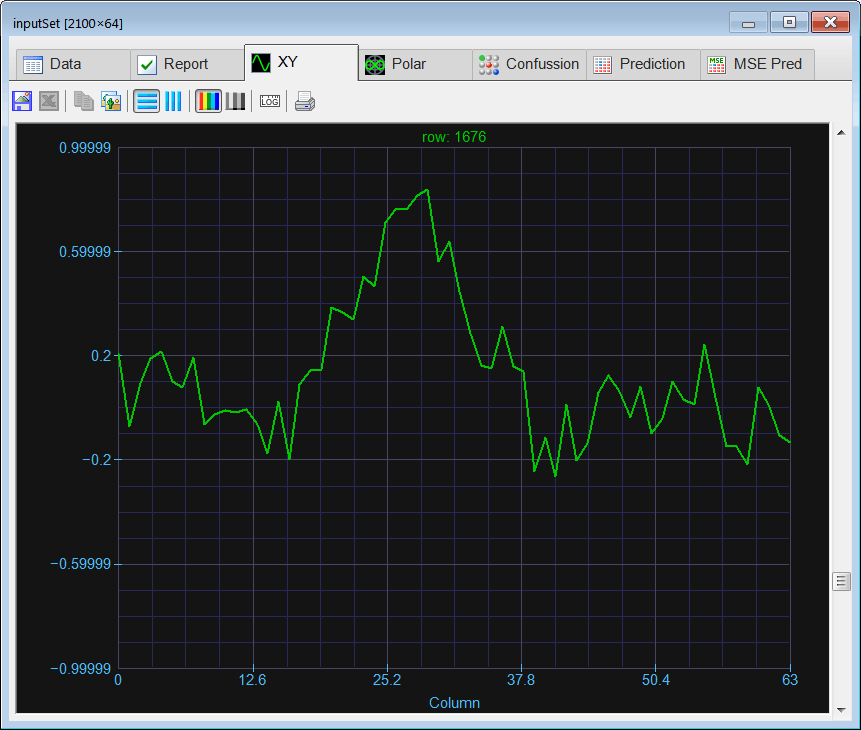
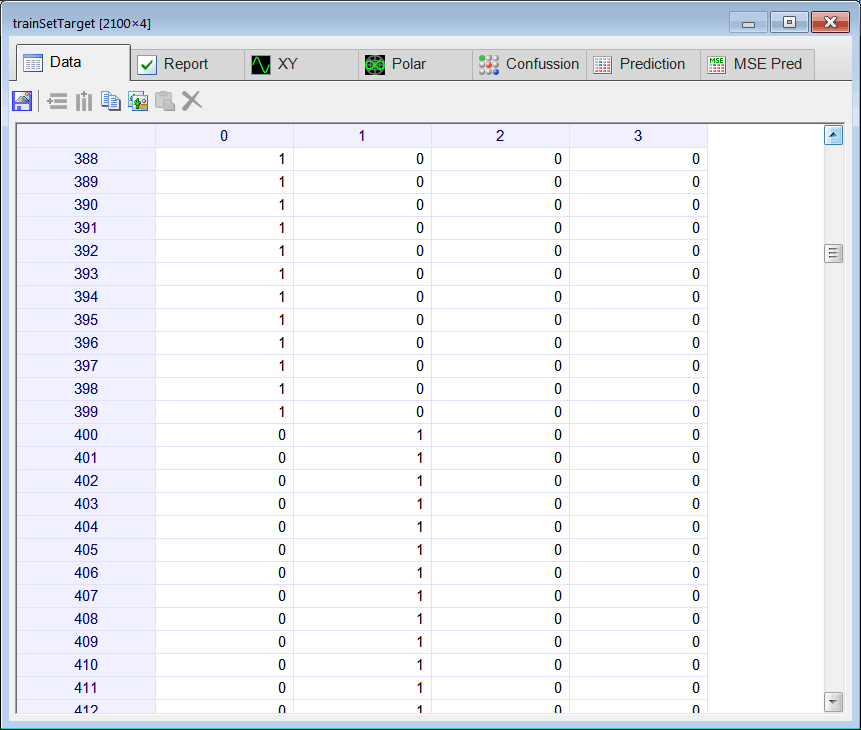
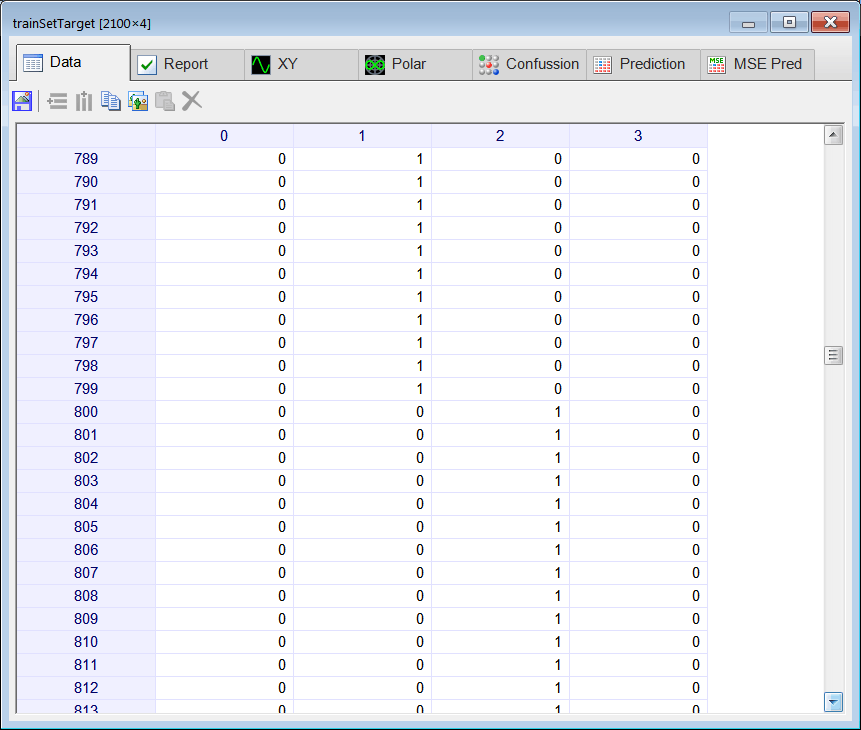
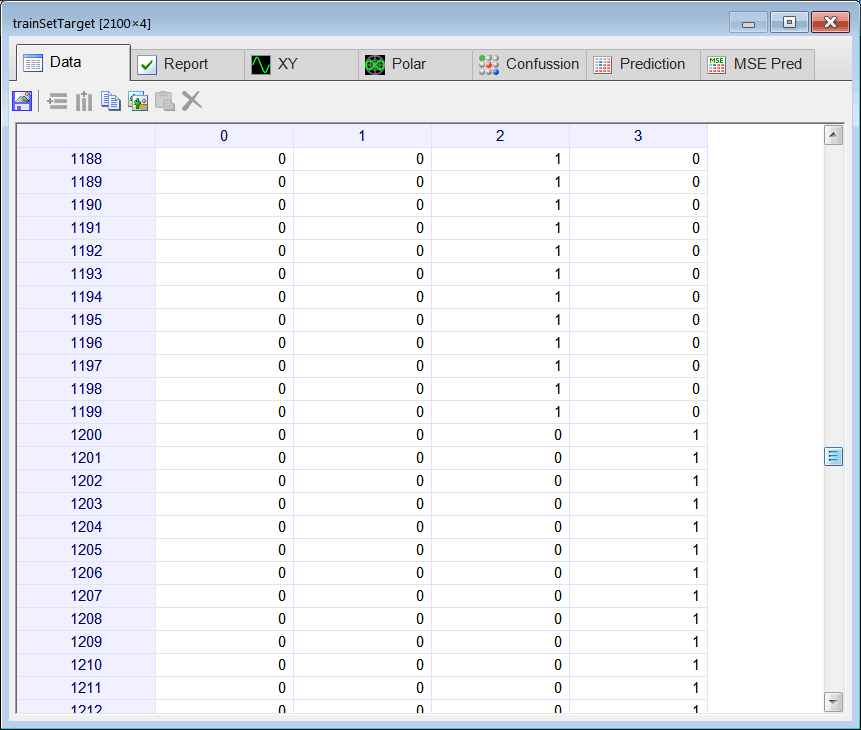
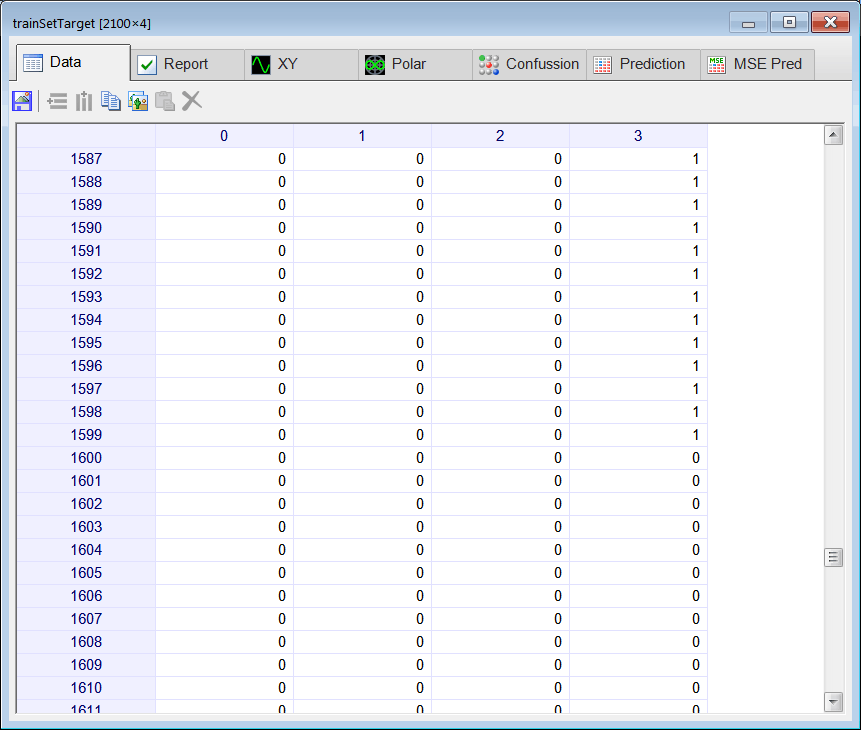
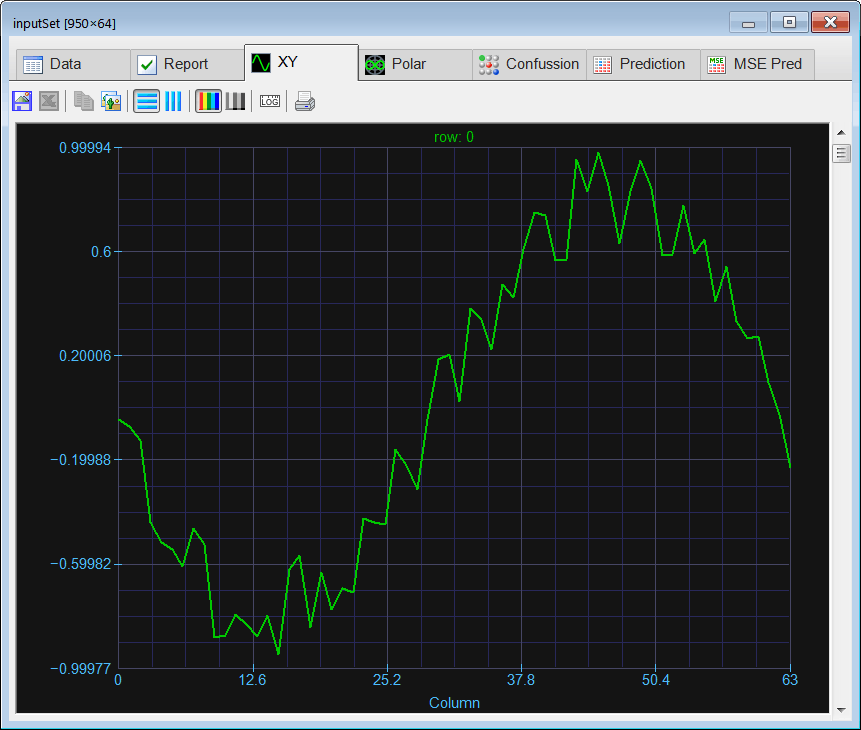
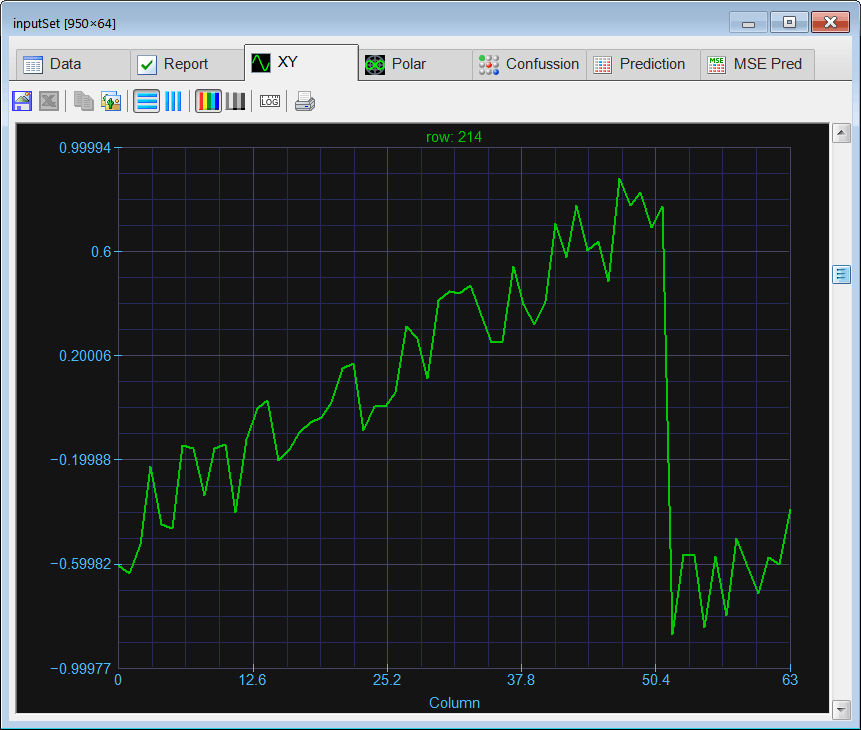
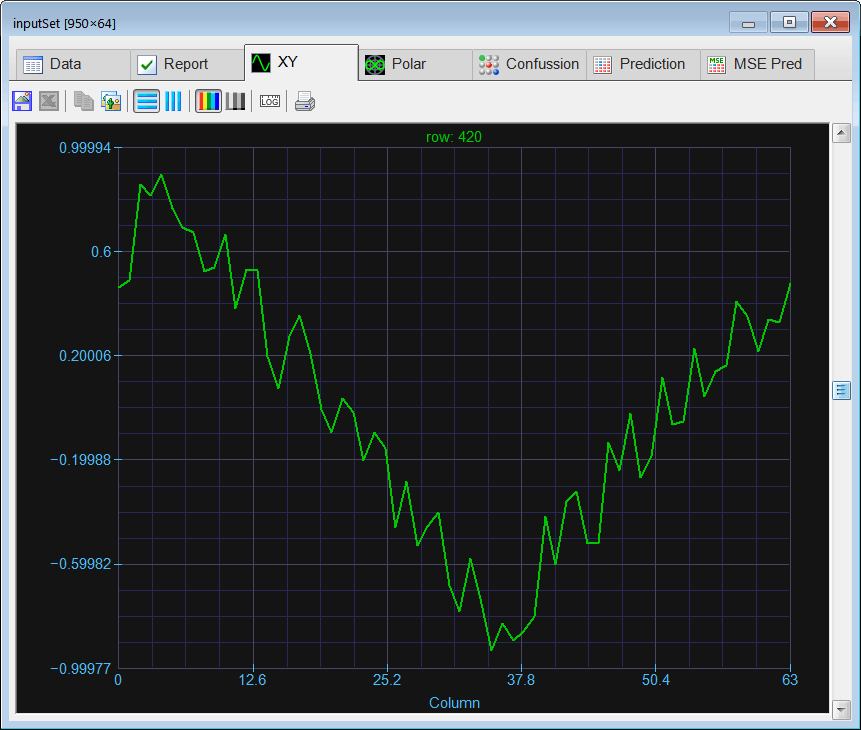
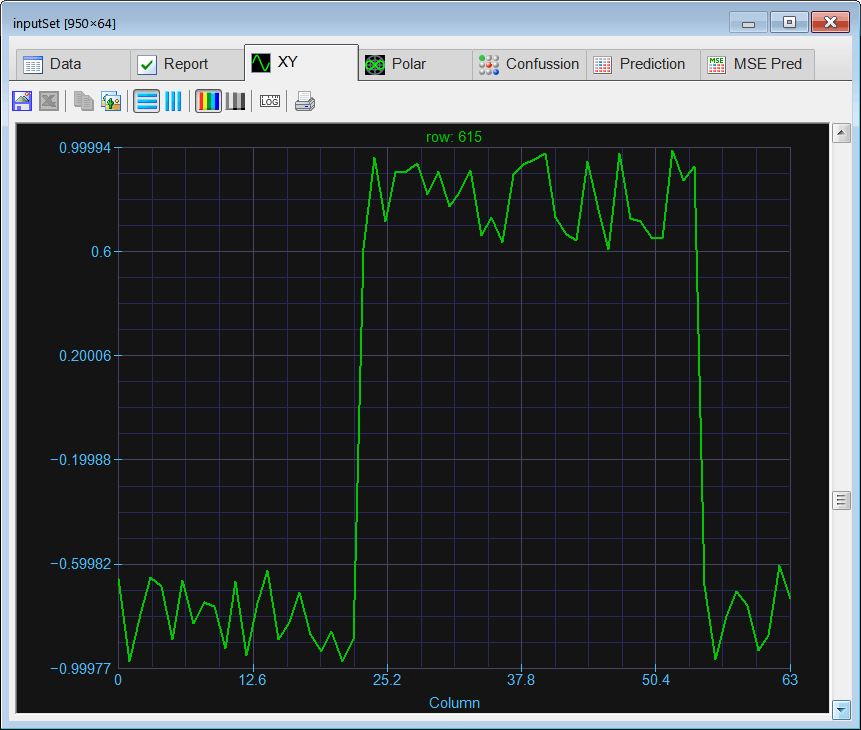
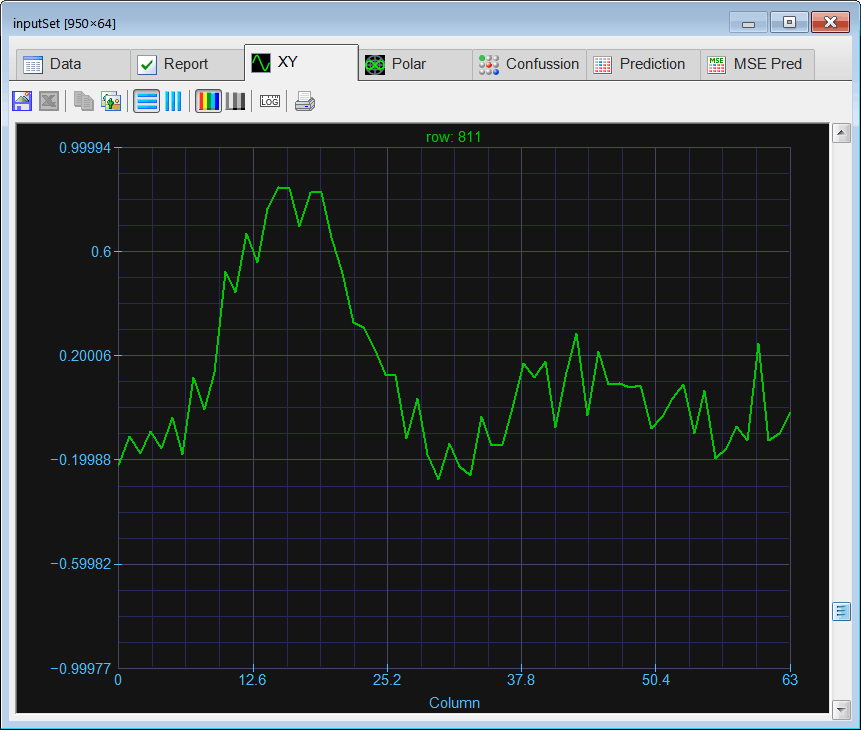
| Create a Neural Lab project called ComplexClass to classify signals in the time domain and in the frequency domain (you may select the Classification option for the network application). Build an appropriate training set for the classification of four noisy signals: the sine, the saw tooth, the triangular, and the squared. These signals will be contaminated with 20% of noise. The input training set must include 400 waves of each class and 500 additional cases for the sinc function for rejection. Use 2100 training cases and 64 inputs. Each training case has a wave with a random phase. Note that the training set target has only four columns. (You may use code from the problem Neural Lab > Classification > Noisy Classification ) |
| ComplexClass\BuildTrainSet.lab |
| int numCases = 400; int numInputs = 64; double deltaInput = 6.28/numInputs; int i; int j; double phase = 0.0; //________________________________ Class 1: sine Matrix inputSine; ... } //________________________________ Class 2: sawtooth Matrix inputSaw; ... } //________________________________ Class 3: triangular Matrix inputTria; ... //________________________________ Class 4: squared Matrix inputSqu; ... //________________________________ Reject: sinc Matrix inputSinc; ... //_______________________________ Create the inputSet Matrix inputSet; ... Matrix noise; noise.CreateRandom(inputSet.GetRowCount(), inputSet.GetColCount(), -1.0, 1.0); trainSetInput = 0.8*inputSet + 0.2*noise; inputSet.Save(); //_______________________________ Create the training set target Matrix trainSetTarget; ... trainSetTarget.Save(); //_____________________________ Save the training set input for the complex domain network ComplexMatrix trainSetInputCx = fft(inputSet); //Delete half of the transformed data int numCols = trainSetInputCx.GetColCount(); Vector index; index.CreateSeries(numCols/2, numCols-1, numCols/2); trainSetInputCx.DeleteCols(index); trainSetInputCx.Save(); //_____________________________ Save the training set input for the real domain network Matrix trainSetInput = realfft(inputSet); trainSetInput.Save(); |
| Problem 2 |
| Build an appropriate validation set for classification of the noisy four signals. Use 950 validation cases (200 cases for each class and 150 for rejection). The validation set must contain signals contaminated with 20% of noise. |
| Problem 3 |
| When using the FFT to solve a classification problem, should we apply the same scaling to all ANN inputs or should we scale each input separately? |
| Tip |
| A CSV file can store a Matrix or a ComplexMatrix as a coma separated value. As the CSV file is a text file, you can save a Matrix to a CSV file, and then load the same matrix as a ComplexMatrix. |
| Problem 4 |
| Edit the Train.lab file to design and train an ANN for classification of the four signals in the frequency domain using the function: realfft. Observe that this function returns the real and imaginary values stored sequentially, thus, the first input of the ANN takes the real part of the first complex value, the second input takes the imaginary part of the first complex value, etc. For instance suppose that the FFT is: 2+4j, 8+5j,..., 7+10j, then realfft will return 2, 4, 8, 5, ..., 7, 10. |
| ComplexClass\Train.lab |
| //_________________________ Network Setup LayerNet net; net.Create(64, 12, 0, 4); int i = 0; //____________________________ Input Scaling for(i = 0; i<64; i++) { //net.SetInScaler(i, -17, 15); // Input values are from -17 to 15 net.SetInScaler(i, -35, 35); } //____________________________ Output Scaling for(i = 0; i<4; i++) { net.SetOutScaler(i, 0.0, 1.0); // Output values are from 0 to 1 } //________________________ Load and set the training set Matrix trainSetInput; trainSetInput.Load(); Matrix trainSetTarget; trainSetTarget.Load(); net.SetTrainSet(trainSetInput, trainSetTarget, false); //________________________ Train net.TrainSimAnneal(100, 100, 15, 0.01, false, 4, 1.0e-12); net.TrainConjGrad(2500,1.0e-12); //_____________________________ Save the trained network net.Save(); |
| Problem 5 |
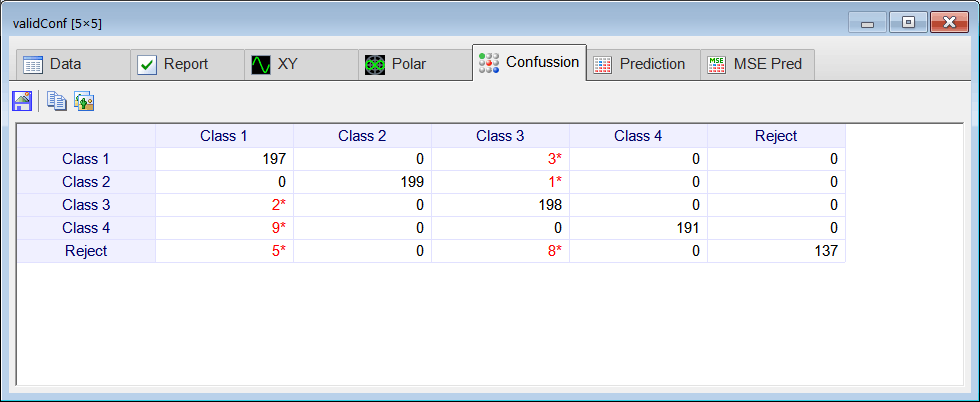
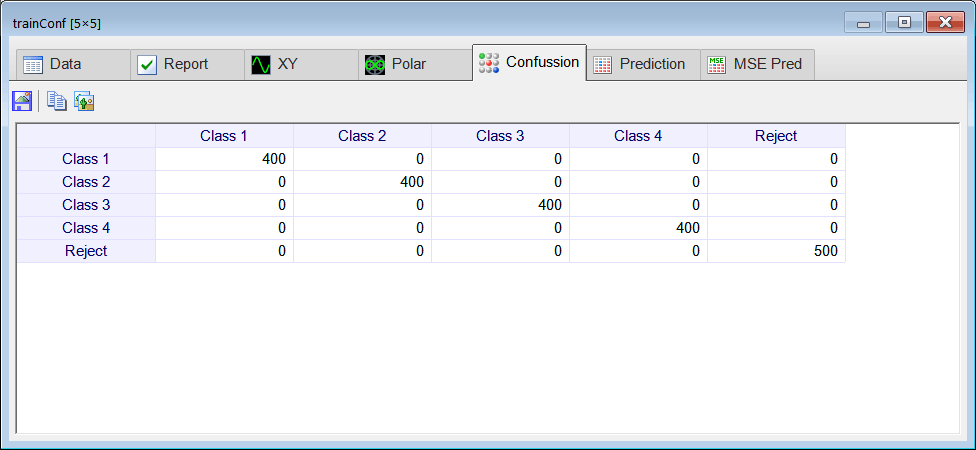
| Edit the CheckTraining.lab file to check the training: (a) Compute the confusion matrix for the ANN using the training set. (b) Plot the error for each network output. (c) Save the confusion matrix as a vector image (trainConf.emf). |
| ComplexClass\CheckTraining.lab |
| //_________________________________________ Load the Training Set Matrix trainSetInput; trainSetInput.Load(); Matrix trainSetTarget; trainSetTarget.Load(); //_________________________________________ Load the ANN LayerNet net; net.Load(); //_________________________________________ Run Matrix output = net.Run(trainSetInput); //_________________________________________ Compute the Confusion Matrix Matrix trainConf = ConfusionMatrix(output, trainSetTarget, 0.5); trainConf.Save(); //_________________________________________ Compute the Number of Errors int numErrors = toint(trainConf.GetSum()) - toint(trainConf.GetDiagonalSum()); |
| Problem 6 |
| Edit the Validation.lab file to perform the validation of the ANN. (a) Compute the confusion matrix for the ANN using the validation set. (b) Plot the error for each network output. (c) Save the confusion matrix as a vector image (validConf.emf). |
| ComplexClass\Validation.lab |
| //_________________________________________ Load the validation set Matrix validSetInput; validSetInput.Load(); Matrix validSetTarget; validSetTarget.Load(); //_________________________________________ Load the ANN LayerNet net; net.Load(); //_________________________________________ Run Matrix output = net.Run(validSetInput); //_________________________________________ Compute the confusion matrix Matrix validConf = ConfusionMatrix(output, validSetTarget, 0.5); validConf.Save(); //_________________________________________ Compute the Number of Errors int numErrors = toint(validConf.GetSum()) - toint(validConf.GetDiagonalSum()); |