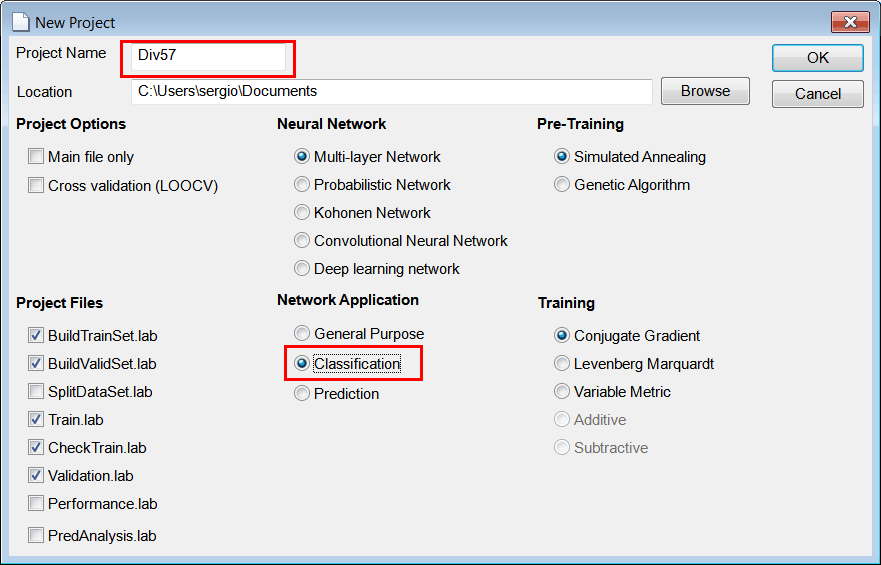
//_________________________ Network Setup
LayerNet net;
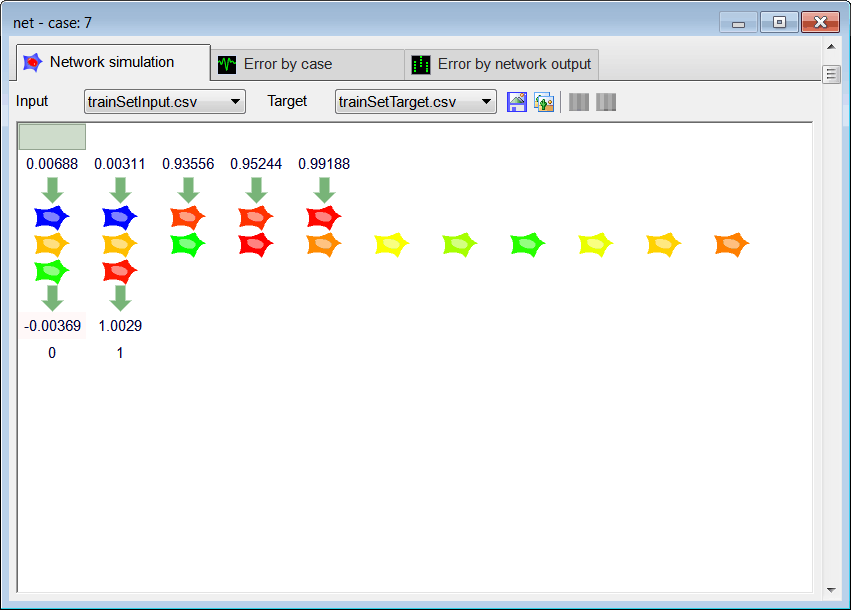
net.Create(5, 1, 0, 2); // 2 Outputs means 2 Classes
//____________________________ Input Scaling
net.SetInScaler(0, 0.0, 1.0);
net.SetInScaler(1, 0.0, 1.0);
net.SetInScaler(2, 0.0, 1.0);
net.SetInScaler(3, 0.0, 1.0);
net.SetInScaler(4, 0.0, 1.0);
//____________________________ Output Scaling
net.SetOutScaler(0, 0.0, 1.0);
net.SetOutScaler(1, 0.0, 1.0);
//________________________ Load and set the training set
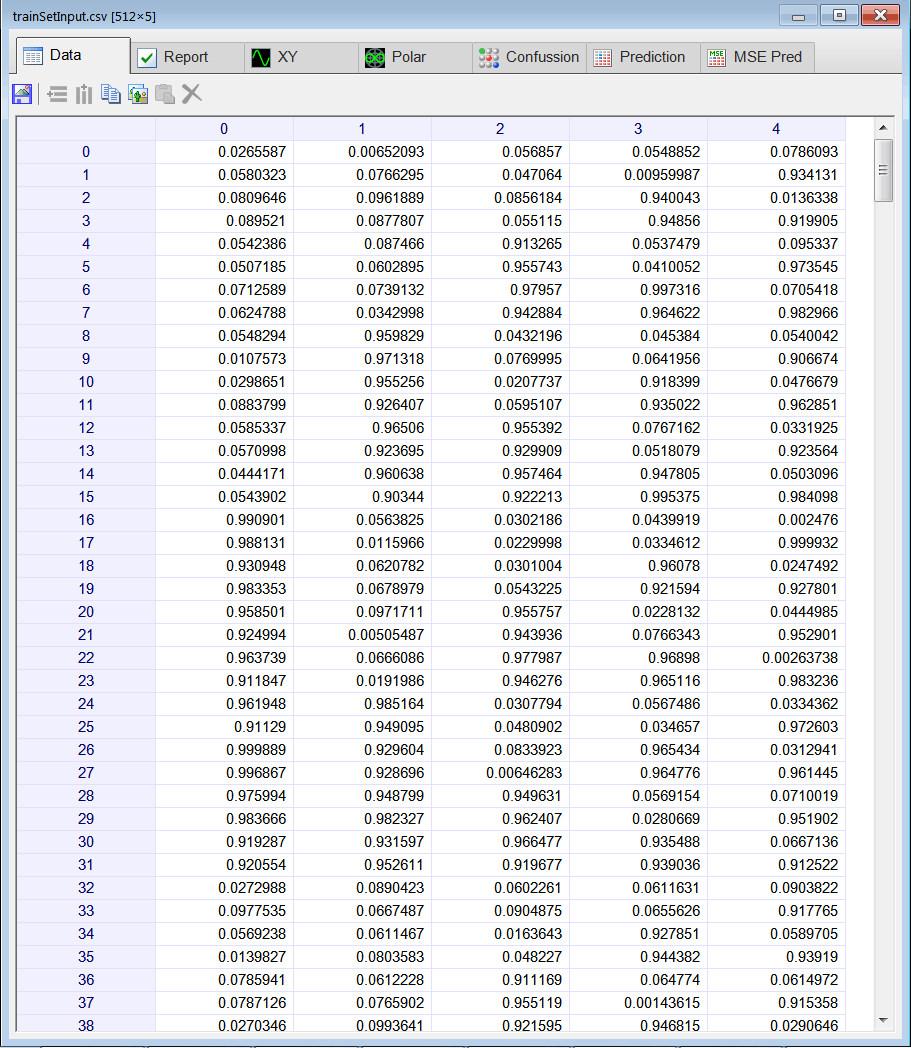
Matrix trainSetInput;
trainSetInput.Load();
Matrix trainSetTarget;
trainSetTarget.Load();
net.SetTrainSet(trainSetInput, trainSetTarget, false);
//________________________ Train
net.TrainSimAnneal(10, 20, 15, 0.001, false, 4, 1.0e-12);
net.TrainLevenMar(2000,1.0e-12);
//_____________________________ Save the trained network
net.Save();
|
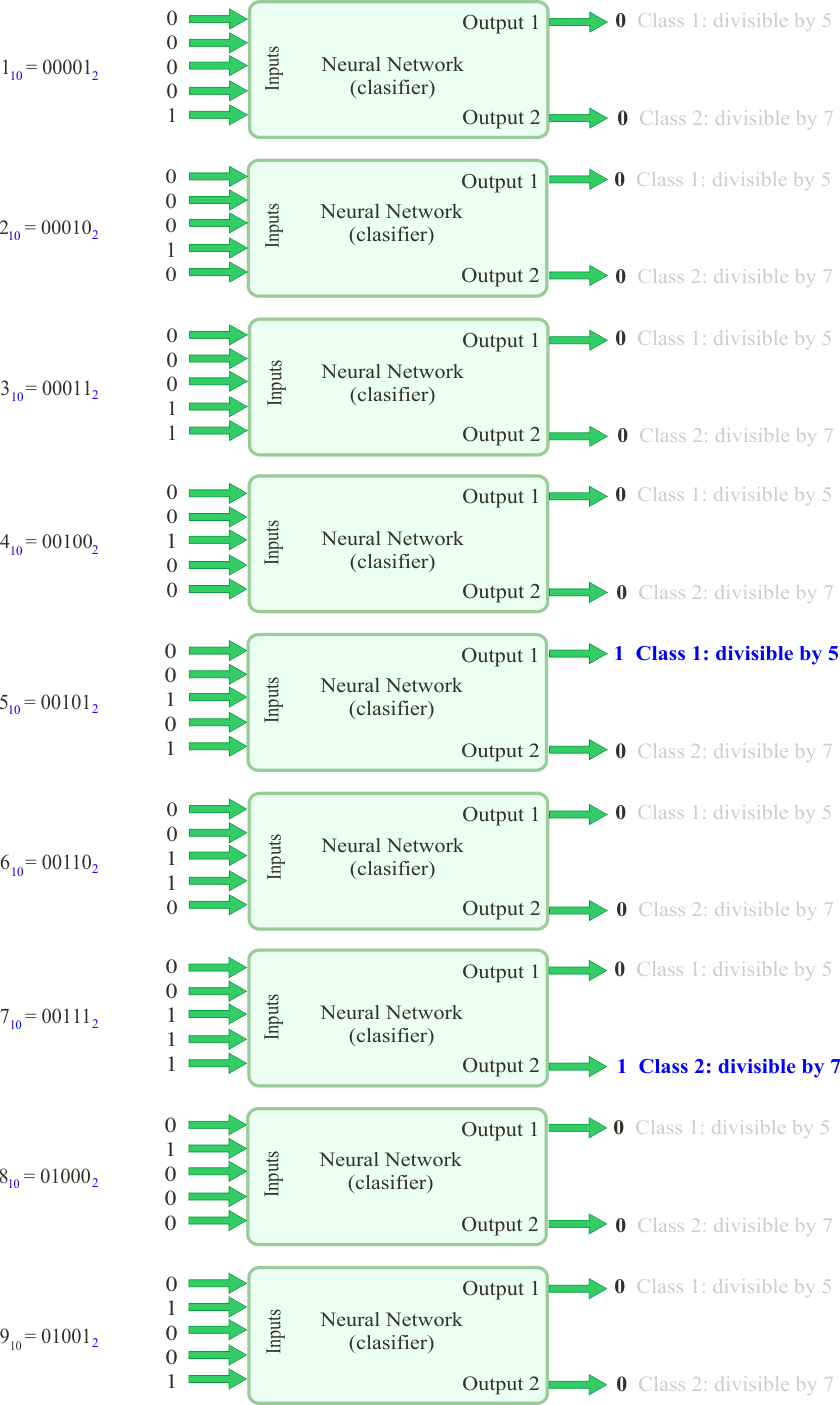
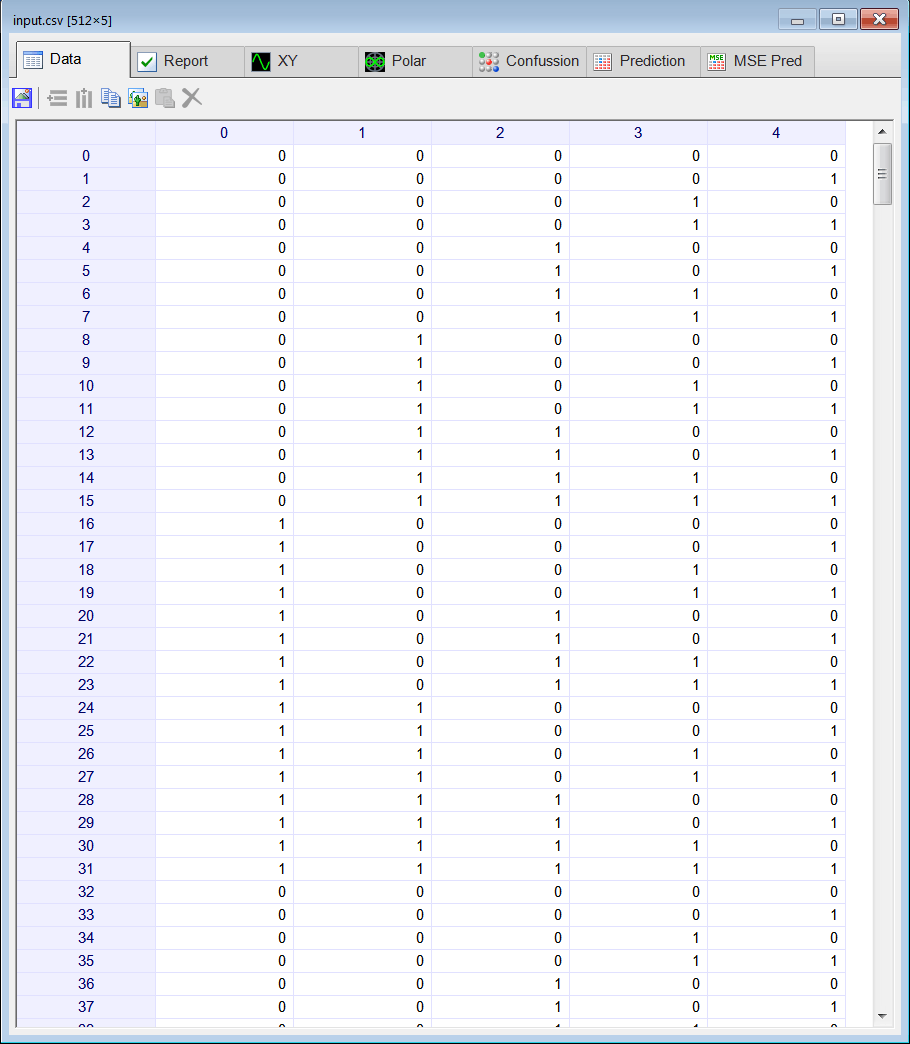
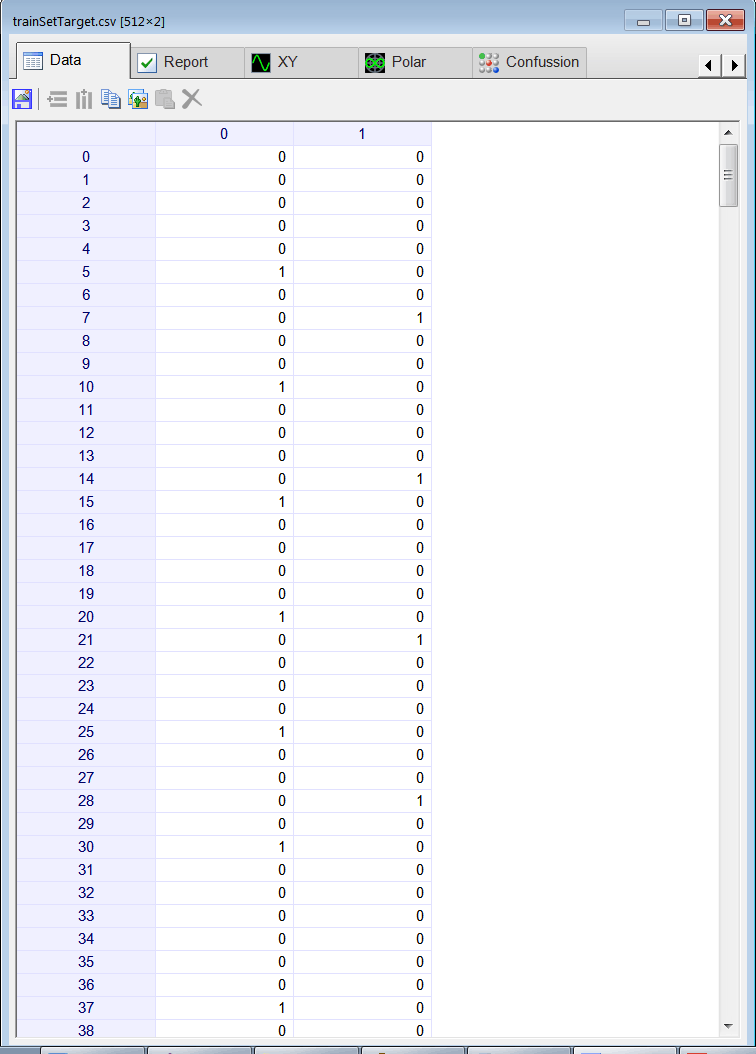
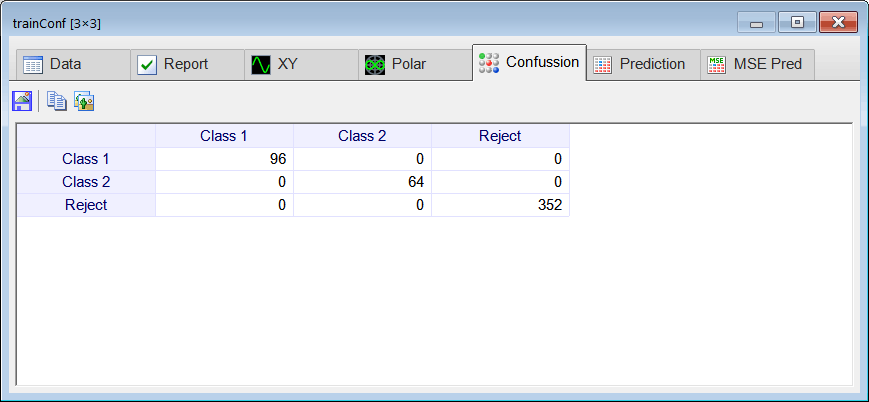
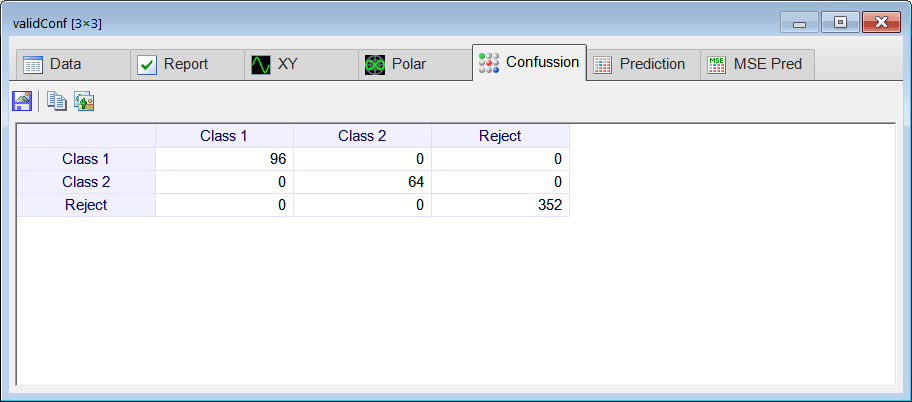
 Runclick the button to execute the code. If you do not have any errors, the training set will be generated and displayed on the variable list and the file list. Click on the file to see its contents. The first 32 rows of the training set are the binary representation of the numbers from 0 to 31; the second 31 rows of the training set are again the representation of the number from 0 to 31. The training set target has two columns, the first column is for class 1 (divisible by 5) and the second column is for class 2 (divisible by 7).
Runclick the button to execute the code. If you do not have any errors, the training set will be generated and displayed on the variable list and the file list. Click on the file to see its contents. The first 32 rows of the training set are the binary representation of the numbers from 0 to 31; the second 31 rows of the training set are again the representation of the number from 0 to 31. The training set target has two columns, the first column is for class 1 (divisible by 5) and the second column is for class 2 (divisible by 7).