| Tip |
| One of the main advantages of working with periodic signals is that their spectrum is limited to some frequencies. On the other hand, non-periodic signals may exhibit broad and complex spectrums that make noise reduction by filtering challenging. For this kind of signals, ANNs are a good option as they may adapt to any kind of signals and any kind of noise. Generally, the training set of non-periodic signals must contain more training cases than the training set of periodic signals. |
| Problem 1 |
| Create a New Project called AutoSinc to build an appropriate training set for learning of the sinc signal z = sinc(x) using an ANN for auto-association as shown in the figure. Use an appropriate number of training cases and inputs. To contaminate the sinc signal, the noise must have the same amplitude properties of the sinc signal (take into consideration that the sinc function goes from -0.2173 to 1.0) |
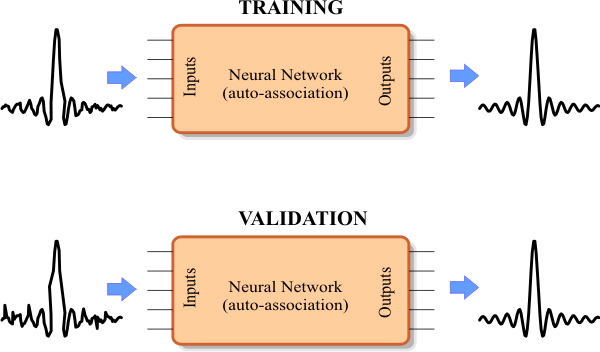
| Problem 2 |
| Edit the BuildValidSet.lab file to build the validation set using the training set. Contaminate the target training set with 10% of noise to create the validation set input. The target of the validation set is the same as the target of the training set. |
| Problem 3 |
| Edit the Train.lab file to design and train an ANN for z = sinc(x). Design the type of training and the training parameters to get the best results. |
| Problem 4 |
| Edit the CheckTraining.lab file to check the training: (a) Compute the mean squared error for the ANN using the training set. (b) Plot the error for each training case. (c) Save the plot as a vector image (checkTraining.pdf and checkTraining.emf) |
| Problem 5 |
| Edit the Validation.lab file to perform the validation of the ANN. (a) Compute the mean squared error for the ANN using the validation set. (b) Plot the error for each validation case. (c) Save the plot as a vector image (validation.pdf and validation.emf) |
| Problem 6 |
| Generate a report in Microsoft Word. Write some conclusions in the report focusing on the problems that were faced during the simulation and how these problems were or could be solved. |