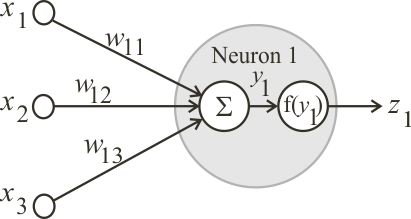
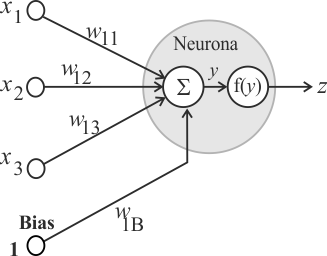
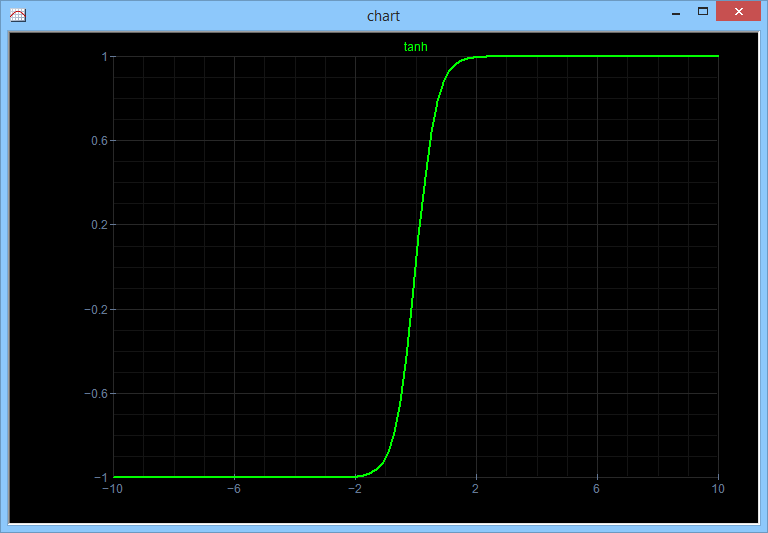
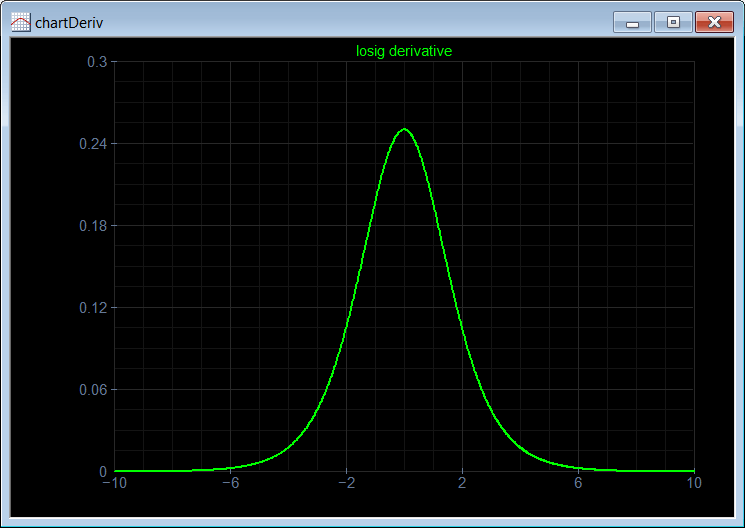
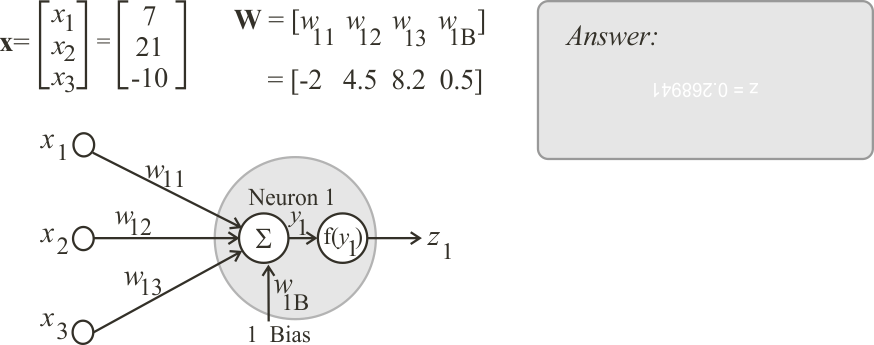
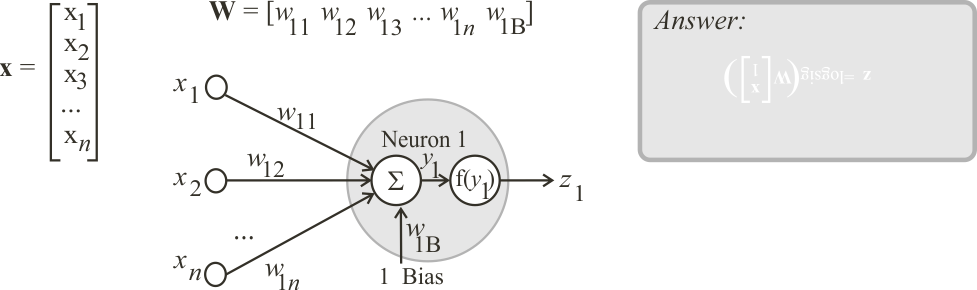
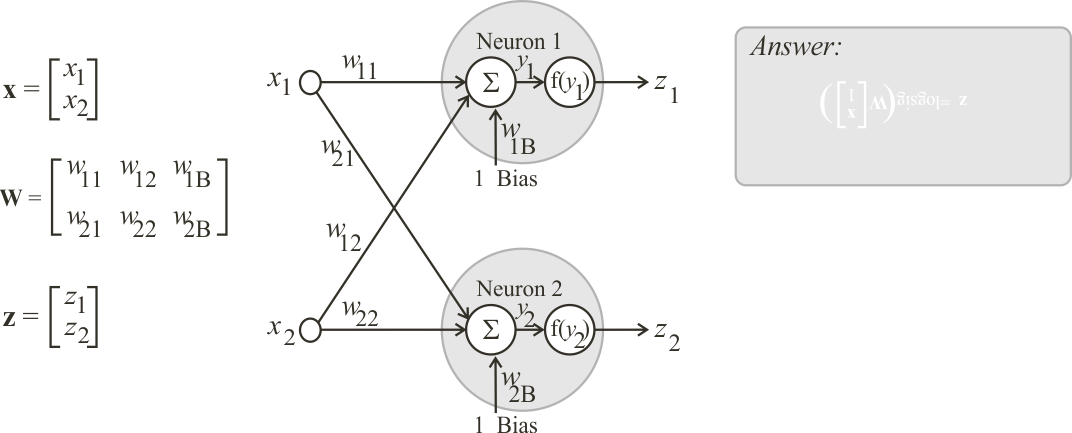
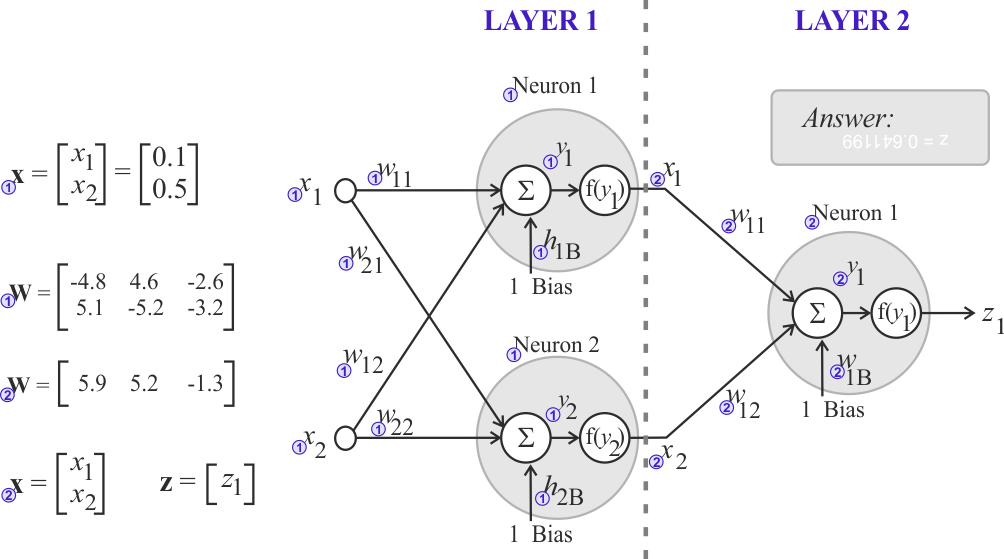
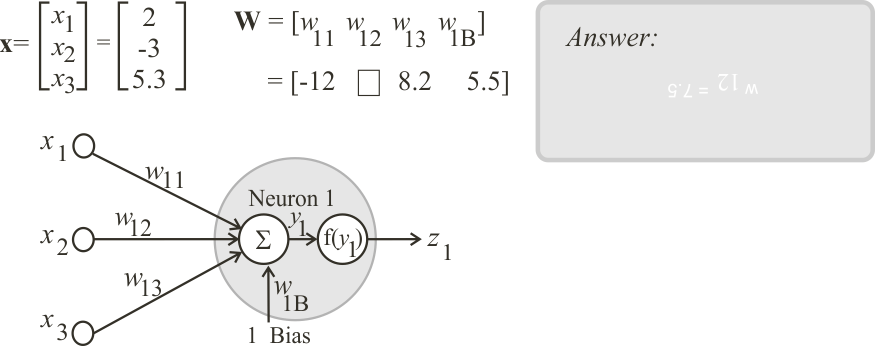
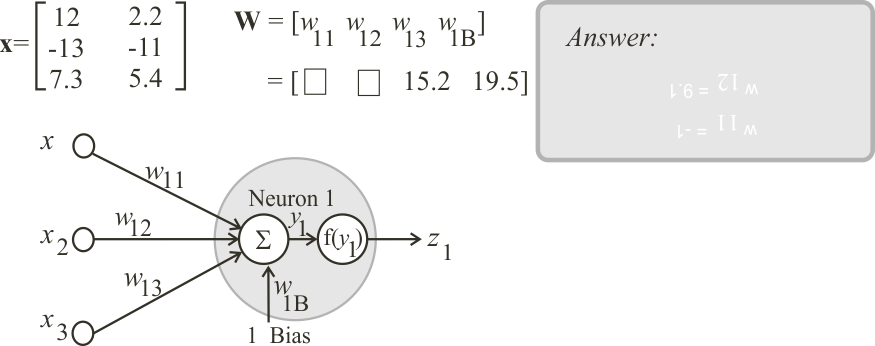
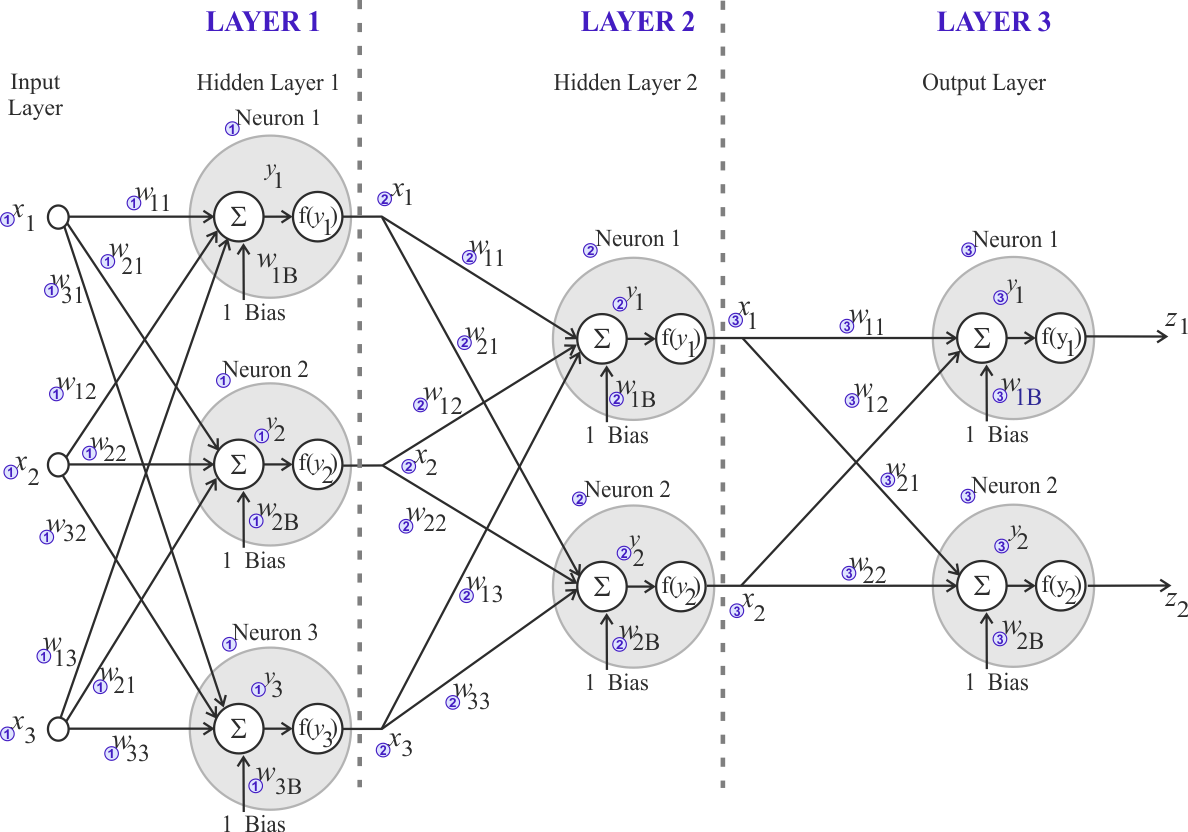
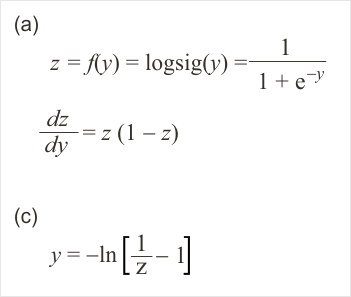Neural Lab open Neural Lab and click on
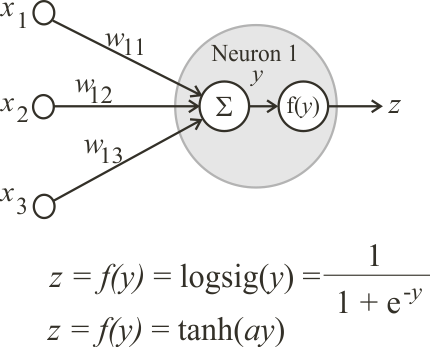
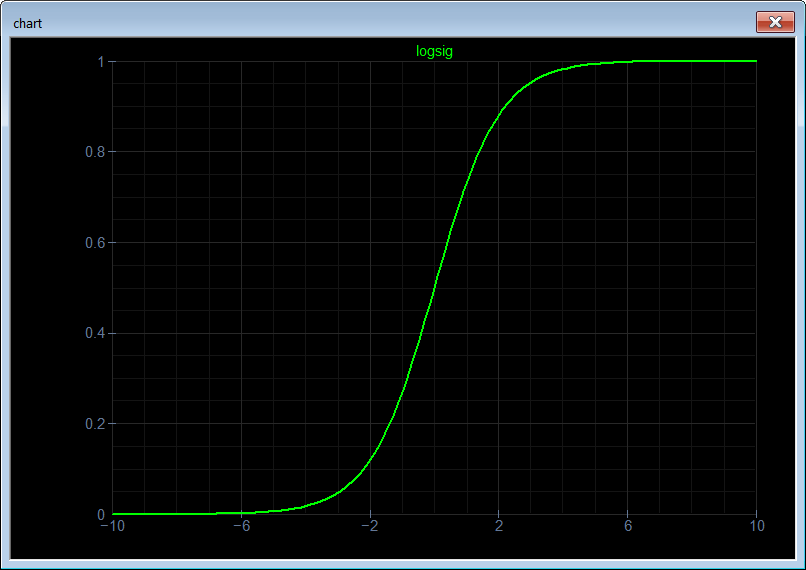
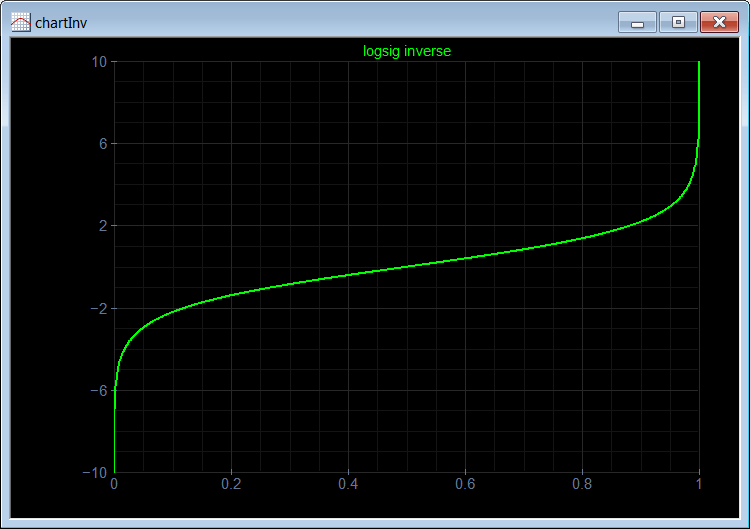
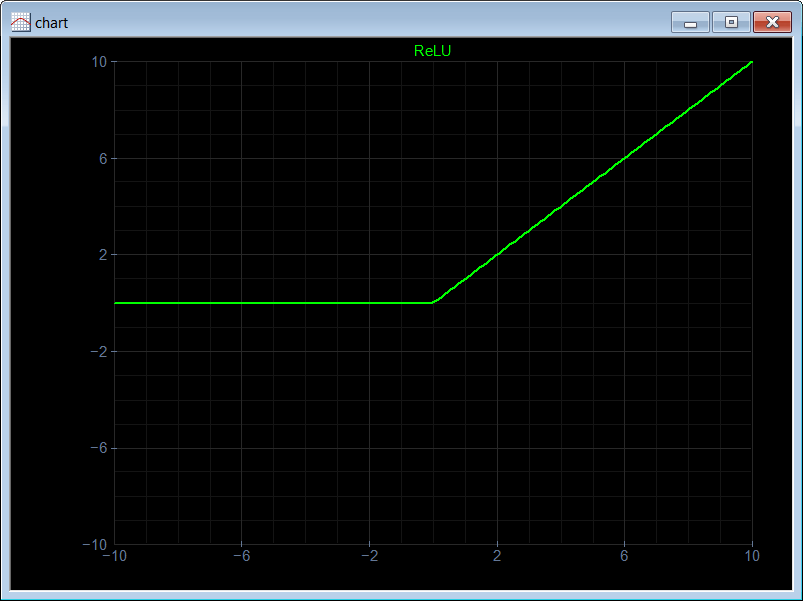
Neural Lab open Neural Lab and click on  New Project. Set the project name to Logsig and select the Main file only option. Then write the code show below. The code begins by creating a vector y of length 100 with values from -10.0 to 10.0. Then, another vector z is computed using the equation of the logsig function. The code ends by creating a XyChart that will be displayed and saved to disk.
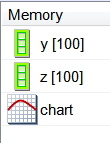
New Project. Set the project name to Logsig and select the Main file only option. Then write the code show below. The code begins by creating a vector y of length 100 with values from -10.0 to 10.0. Then, another vector z is computed using the equation of the logsig function. The code ends by creating a XyChart that will be displayed and saved to disk. Run press the button to run the code. If you do not have any errors, the variables y and z will be displayed in the variable list and the graph will be displayed.
Run press the button to run the code. If you do not have any errors, the variables y and z will be displayed in the variable list and the graph will be displayed.